Układy równań – zadania z egzaminów gimnazjalnych
Na statku wycieczkowym są 33 miejsca dla pasażerów. Uczniowie klas IIIa i IIIb planują wycieczkę tym statkiem. W każdej z tych klas jest mniej niż 33 uczniów. Aby wszystkie miejsca dla pasażerów były na statku zajęte, należy do wszystkich uczniów klasy IIIa dołączyć \(\frac{1}{3}\)uczniów klasy IIIb albo do wszystkich uczniów klasy IIIb dołączyć \(\frac{1}{4}\) uczniów klasy IIIa. Ilu uczniów jest w każdej z tych klas? Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Para liczb (3, –2) spełnia układ równań
Do przewiezienia 27 ton żwiru potrzeba 5 małych i 2 dużych ciężarówek albo 3 małych i 3 dużych ciężarówek (przy wykorzystaniu całkowitej ich ładowności). Ile co najmniej kursów musi wykonać jedna duża ciężarówka, aby przewieźć 27 ton żwiru? Zapisz obliczenia.
Maja, Ola i Jagna kupowały zeszyty. Maja za 3 grube zeszyty i 8 cienkich zapłaciła 10 zł. Ola kupiła 4 grube oraz 4 cienkie zeszyty i również zapłaciła 10 zł. Czy Jagnie wystarczy 10 złotych na zakup 5 grubych zeszytów i 1 cienkiego? Zapisz obliczenia i odpowiedź.
Zmieszano dwa gatunki herbaty, droższą i tańszą, w stosunku 2:3. Cena jednego kilograma tej herbacianej mieszanki wynosi 100 zł. Gdyby ty herbaty zmieszano w stosunku 1:4, to cena za 1 kg tej mieszanki wynosiła by 80 zł. Na podstawie podanych informacji zapisano poniższy układ równań.
\(\left\{ \begin{matrix} \frac{2}{5}x+\frac{3}{5}y=110 \\ \frac{1}{5}x+\frac{4}{5}y=80 \\ \end{matrix} \right.\)Co oznacza x w tym układzie równań? Wybierz właściwą odpowiedź spośród podanych.
Rozwiązanie:
Obejrzyj film z wytłumaczeniem.
Odp.: A. Cenę 1 kg herbaty droższej.
Ania ma w skarbonce 99 zł w monetach o nominałach 2 zł i 5 zł. Monet dwuzłotowych jest 2 razy więcej niż pięciozłotowych.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli przez x oznaczymy liczbę monet pięciozłotowych, a przez y – liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
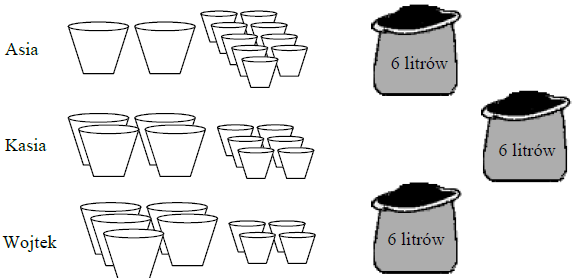
Asia, Kasia i Wojtek przesadzają kwiatki do doniczek. Każde z nich ma 6-litrowy worek ziemi ogrodniczej i doniczki dwóch wielkości. Asia wykorzystała całą ziemię, którą dysponowała, i napełniła 2 duże doniczki i 9 małych. Kasia całą swoją ziemię zużyła do wypełnienia 4 dużych i 6 małych doniczek. Wojtek chciałby wypełnić ziemią 5 dużych i 4 małe doniczki. Czy wystarczy mu ziemi, którą ma w worku? Uzasadnij odpowiedź.
Maksymalnie załadowane ciężarówki: jedna o nośności 8 t, a druga 12 t przewiozły 520 ton węgla, wykonując w sumie 60 kursów. Ułóż układ równań, który pozwoli obliczyć, ile kursów wykonała każda z ciężarówek.




