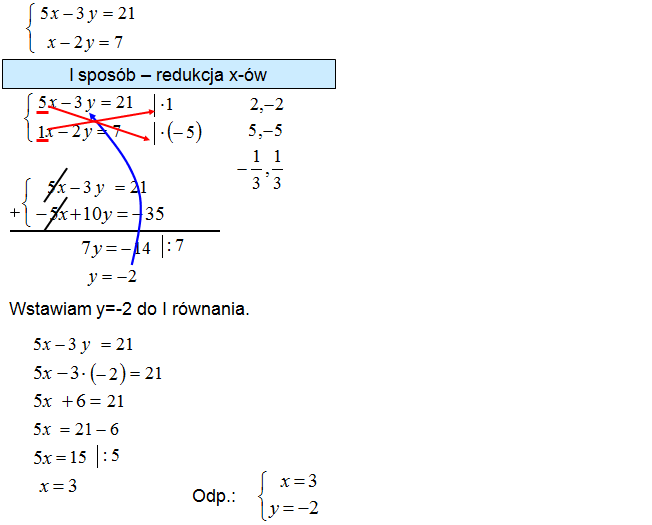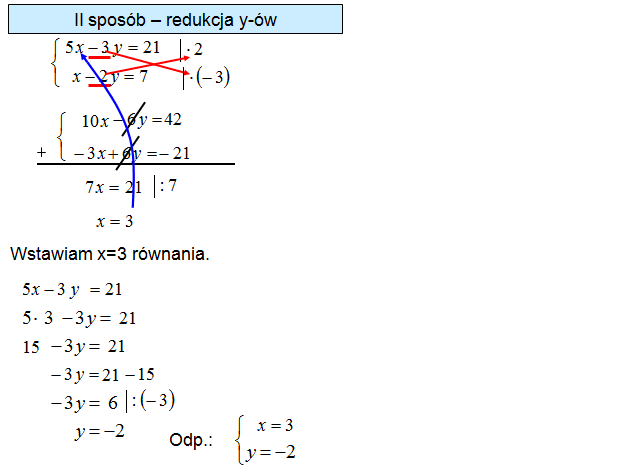Rozwiąż układ równań metodą przeciwnych współczynników
Metoda przeciwnych współczynników polega na znalezieniu lub utworzeniu przeciwnych współczynników przy tych samych niewiadomych x lub y.
Przykłady liczb przeciwnych – przeciwnych współczynników:
3 i -3;
7 i -7;
-2 i 2 itp.
Teraz rozwiążemy krok po kroku układ równań metodą przeciwnych współczynników.
Krok 1: Przyglądasz się i sprawdzasz, czy w układzie równań przy tych samych niewiadomych są już przeciwne liczby – przeciwne współczynniki. Jeśli są przejdź do kroku 3. W przeciwnym przypadku należy pomnożyć układ po skosie tak jak pokazuje rysunek z kroku 1. Jeśli chcesz redukować niewiadome x, wówczas mnożysz I równanie przez współczynnik stojący przy zmiennej x z II równania. II równanie mnożysz przez współczynnik stojący przy niewiadomej x z I równania. Oczywiście mnożenie przez liczbę 1 nie ma sensu, ale warto ją zapisać dla wytłumaczenia sensu metody przeciwnych współczynników.
Uwaga: Mnożąc układ „po skosie”, czasem należy dopisać znak minusa „-” przy jednej z liczb mnożących całe równanie. Znak minusa dopisujesz, gdy widzisz, że po wymnożeniu otrzymasz takie same współczynniki przy wybranej niewiadomej. W naszym przypadku dopisałem znak „-” do liczby wymnażającej II równanie. Widzisz zamiast liczby „5” napisałem liczbę „-5”. Teraz metoda przeciwnych współczynników będzie miała sens, bo powstaną przeciwne liczby przy tych samych niewiadomych.
W tym przykładzie zechcemy zredukować zmienną x. Musisz utworzyć przeciwne współczynniki, przeciwne liczby właśnie przy x-ach.
Na początku poznawania metody podstawiania radzę pomnożyć układ równań po skosie według podanego niżej schematu dodając czasem minus do liczby wymnażającej dane równanie.
W pierwszym równaniu przy x stoi liczba 5, zatem drugie równanie mnożysz przez „5”. W drugim równaniu przy x stoi „1” zatem pierwsze równie pomnożymy przez „1”. Zauważamy jednak, że po wymnożeniu oba równania będą zaczynały się od jednomianu „5x”. My zaś chcemy, aby powstały przeciwne współczynniki zatem w jednym z równań trzeba dodatkowo zmienić znaki. Więc drugie równanie nie będziemy mnożyć przez „5” tylko przez „-5”.

Krok 2: Wymnażasz układ równań i zauważasz przeciwne liczby, przeciwne współczynniki przy niewiadomej x.

Krok 3:Teraz podkreślasz układ równań i dodajesz równania stronami. Lewą stronę dodajesz do lewej, a prawą do prawej. Widać, że wyrażenia „5x” i „-5x” można skreślić (zredukować). Jednomiany ze zmienną y dodajemy, redukujemy ze sobą, a z prawej strony redukujemy liczby. Następnie rozwiązujesz proste równanie z jedną niewiadomą dzieląc równanie stronami przez liczbę stojącą przy niewiadomej. Otrzymujesz w efekcie y=-2.
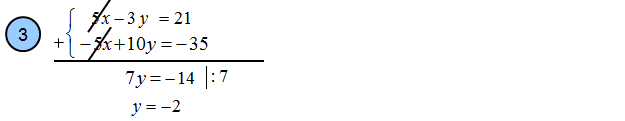
Krok 4: Otrzymaną liczbę „-2” wstawiasz do pierwszego lub drugiego równania z naszego przykładu. Jeśli nie rozumiesz przepisz teraz pierwsze równanie ołówkiem. Następnie zetrzyj literkę „y”, a w jej miejsce wstaw liczbę „-2”. W tym momencie otrzymasz dość proste równanie z jedną niewiadomą x.
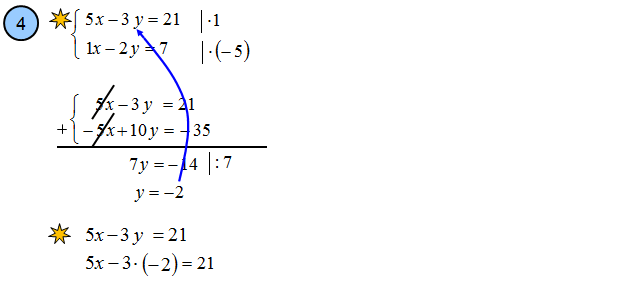
Krok 5: Rozwiązujesz równanie z jedną niewiadomą

Krok 6: Na końcu podajesz odpowiedź łącząc x i y klamerkami.

Znajdź interesujące Ciebie przykłady i rozwiąż układ równań metodą przeciwnych współczynników.
Porównując rozwiązywanie układów metodą podstawiania i przeciwnych współczynników muszę stwierdzić, że osobiście wolę rozwiązywać układy metodą przeciwnych współczynników, ponieważ z reguły jest krótsza. Metoda podstawiania zaś jest bardziej skuteczna w skomplikowanych przykładach wychodzących raczej poza poziom gimnazjum.
Rozwiąż układ równań metodą przeciwnych współczynników.
1 Sposób: Redukcja x-ów.
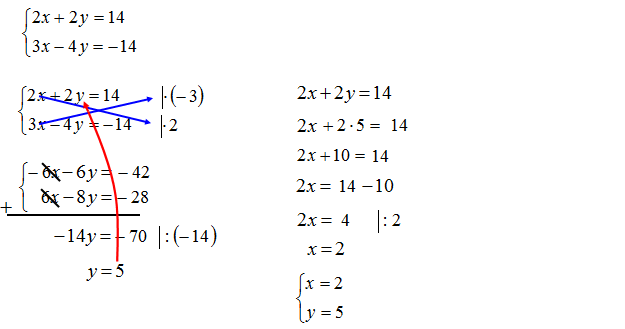
2 Sposób: Redukcja x-ów.
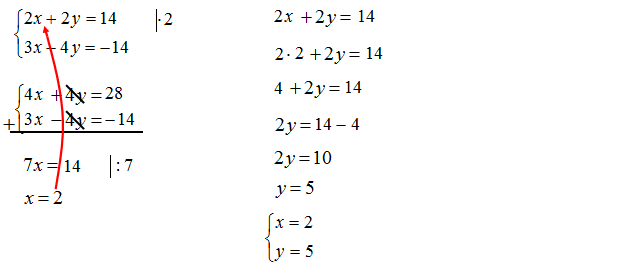
Metoda przeciwnych współczynników w zadaniach i przykładach
Rozwiąż układ równań metodą przeciwnych współczynników.
\[\left\{ {\begin{array}{*{20}{c}} {5x – 3y = – 11}\\ {2x + 4y = 6\quad } \end{array}} \right.\]Rozwiąż układ równań metodą przeciwnych współczynników.
\[\left\{ {\begin{array}{*{20}{c}} {2x – 3y = – 23}\\ {3x + 2y = 17,5} \end{array}} \right.\]Rozwiąż układ równań.
\[\left\{ {\begin{array}{*{20}{c}} {2x + 3y = 8\;}\\ { – 4x + 5y = 6} \end{array}} \right.\]Niekiedy wystarczy pomnożyć tylko jedno równanie, aby otrzymać przeciwne współczynniki. Tutaj pomnóż pierwsze równanie przez liczbę „2”. Wówczas otrzymasz w pierwszym równaniu jednomian „4x”, a w drugim już jest „-4x”. Dalej możesz dodać równania stronami i zredukować przeciwne jednomiany.
Rozwiąż układ równań (Metoda przeciwnych współczynników).
\[\left\{ {\begin{array}{*{20}{c}} {\frac{5}{6}x – \frac{2}{3}y = \frac{5}{3}}\\ {\frac{3}{2}x – y = 2\quad } \end{array}} \right.\]Nie wiem jak Ty, ale ja niezbyt lubię bawić się w ułamkach w układach równań. Co innego, gdy mam liczby całkowite. Zatem w bieżącym układzie usuń na początku mianowniki. Dalej rozwiązujesz standardowo tworząc przeciwne liczby przy tych samych niewiadomych „x” lub „y”.
Rozwiąż układ równań.
\[\left\{ {\begin{array}{*{20}{c}} {\frac{3}{4}x – \frac{4}{5}y = x – y\quad \quad \quad }\\ {3\left( {4 – x} \right) – 5\left( {y – 1} \right) = – 20} \end{array}} \right.\]W pierwszym równaniu usuń mianowniki mnożąc równanie przez wspólny mianownik ułamków będących współczynnikami przy niewiadomych. W drugim równaniu wymnóż nawiasy przez liczby. Dalej upraszczasz układ przenosząc niewiadome x i y na lewą stronę, a liczby na prawą. Mając już uproszczony układ równań możesz zająć się w kolejnym kroku utworzeniem przeciwnych współczynników.