Równania zadania z treścią na egzaminie
Sześć maszyn produkuje pewną partię jednakowych butelek z tworzywa sztucznego przez 4 godziny. Każda z maszyn pracuje z taką samą stałą wydajnością.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
W zawodach sportowych każdy zawodnik miał pokonać trasę składającą się z trzech części. Pierwszą część trasy zawodnik przejechał na rowerze, drugą część − prowadzącą przez jezioro − przepłynął, a trzecią – przebiegł. Na rysunku przedstawiono schemat tej trasy.
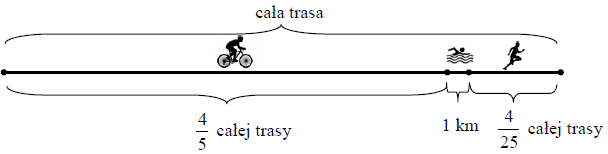
Na podstawie informacji wybierz zdanie prawdziwe.
A. Cała trasa miała długość 50 km.
B. Zawodnik przebiegł 8 km.
C. Odległość, którą zawodnik przebiegł, była o 4 km większa od odległości, którą przepłynął.
D. Odległość, którą zawodnik przejechał na rowerze, była 5 razy większa od odległości, którą przebiegł.
Na rysunku przedstawiono prostokąt, którego wymiary są opisane za pomocą wyrażeń.

Jeden z kątów wewnętrznych trójkąta ma miarę α, drugi ma miarę o 30° większą niż kąt α, a trzeci ma miarę trzy razy większą niż kąt α.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Trójkąt ten jest
A. równoboczny.
B. równoramienny.
C. rozwartokątny.
D. prostokątny.
W pewnej klasie liczba chłopców stanowi 80% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze trzech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Połowa uczestników wycieczki urodziła się w Polsce, co trzeci urodził się w Niemczech, a pięciu pozostałych we Francji. W wycieczce brało udział
A. 26 osób. B. 30 osób. C. 46 osób. D. 60 osób.
Informacje do zadań 8. i 9.
W turnieju szachowym wzięło udział 48 uczniów pewnego gimnazjum. Liczby uczestników turnieju z klas pierwszych, drugich i trzecich są do siebie w proporcji 3 : 8 : 5.
Jaki procent uczestników turnieju stanowili drugoklasiści? Wybierz odpowiedź spośród podanych.
A. 17% B. 24% C. 33% D. 50%
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba uczniów klas pierwszych, którzy wzięli udział w turnieju, jest równa
A. 8 B. 9 C. 10 D. 11
Obwód trapezu równoramiennego jest równy 72 cm, ramię ma długość 20 cm, a różnica długości podstaw wynosi 24 cm. Oblicz pole tego trapezu. Zapisz obliczenia.
Informacje do zadań 1., 2. i 3.
W tabeli przedstawiono średnie zużycie energii przez organizm zawodnika podczas uprawiania wybranych dyscyplin sportowych. Przyjmij, że zużycie energii jest wprost proporcjonalne do czasu.

Ile energii zużywa organizm zawodnika podczas trwającego 1,5 godziny treningu siatkówki?
A. 525 kcal B. 600 kcal C. 700 kcal D. 1050 kcal
Organizm zawodnika podczas trwającego 60 minut treningu zużył 500 kcal. Którą dyscyplinę sportową trenował zawodnik?
A. Piłkę nożną. B. Pływanie. C. Kolarstwo. D. Aerobik.
Podczas treningu piłki nożnej organizm zawodnika zużył 1400 kcal. Ile godzin trwał ten trening?
A. 1,5 B. 2 C. 2,5 D. 3
Energię zużywaną przez organizm człowieka można wyrażać w kilokaloriach (kcal) lub w kilodżulach (kJ). Przyjmij, że 1 kcal = 4,19 kJ. Wskaż prawidłową odpowiedź.
A. 130 kcal to 54,47 kJ
B. 5447 kcal to 130 kJ
C. 130 kcal to 544,7 kJ
D. 544,7 kcal to 130 kJ
Objętość (V) cieczy przepływającej przez rurę o polu przekroju S oblicza się według wzoru V = Svct, gdzie vc oznacza prędkość przepływu cieczy, t – czas przepływu. Który wzór na prędkość cieczy przepływającej przez rurę jest rezultatem poprawnego przekształcenia podanego wzoru?

Trzy lata temu posadzono przed domem krzew. Co roku podwajał on swoją wysokość i teraz ma 144 cm. Jeśli przez x oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie
A. x = 144 B. 4x = 144 C. 6x = 144 D. 8x = 144
Wilgotnością drewna nazywamy stosunek masy wody zawartej w drewnie do masy drewna całkowicie suchego. Przyjęto podawać wilgotność drewna w procentach. Ich liczbę (w) obliczamy za pomocą wzoru:
, gdzie M oznacza masę drewna wilgotnego, a m – masę drewna całkowicie suchego. Wyznacz M w zależności od m i w. Zapisz kolejne przekształcenia wzoru.
W wycieczce rowerowej uczestniczy 32 uczniów. Chłopców jest o 8 więcej, niż dziewcząt. Ilu chłopców jest w tej grupie?
A. 12 B. 16 C. 20 D. 24
Zosia zaoszczędziła 45 zł. Bilet do ogrodu botanicznego kosztuje 10,50 zł. Ile najwięcej biletów może kupić Zosia?
A. 2 B. 3 C. 4 D. 6
Podczas trzydniowej pieszej wycieczki uczniowie przeszli 39 km. Drugiego dnia pokonali dwa razy dłuższą trasę niż pierwszego dnia, a trzeciego o 5 km mniej niż pierwszego. Ile km przebyli pierwszego dnia?
A. 6 B. 11 C. 22 D. 28
Na rzece zbudowano most, który zachodzi na jej brzegi: 150 metrów mostu zachodzi na jeden brzeg, a 1/3 długości mostu na drugi. Oblicz szerokość rzeki, jeżeli stanowi ona 1/6 długości mostu. Zapisz obliczenia.
Jacek i Paweł zbierają znaczki. Jacek ma o 30 znaczków więcej niż Paweł. Razem mają 350 znaczków. Ile znaczków ma Paweł?
A. 145 B. 160 C. 190 D. 205
Paweł kupił australijski znaczek i 3 znaczki krajowe. Każdy znaczek krajowy kosztował tyle samo. Za wszystkie znaczki zapłacił 16 zł. Ile kosztował znaczek australijski, jeżeli był pięciokrotnie droższy niż znaczek krajowy?
A. 4 zł B. 10 zł C. 12 zł D. 13 zł
Do pracowni komputerowej zakupiono 8 nowych monitorów i 6 drukarek za łączną kwotę 9400 zł. Drukarka była o 300 zł tańsza niż monitor. Cenę monitora można obliczyć, rozwiązując równanie:
A. 8x + 6(x + 300) = 9400
B. 8x + 6(x – 300) = 9400
C. 8(x-300) + 6x = 9400
D. 8(x + 300) + 6(x-300) = 9400
Marcin przebywa autobusem 3/4 drogi do jeziora, a pozostałą część piechotą. Oblicz odległość między domem Marcina, a jeziorem, jeżeli trasa, którą przebywa pieszo, jest o 8 km krótsza niż trasa, którą przebywa autobusem. Zapisz obliczenia.




