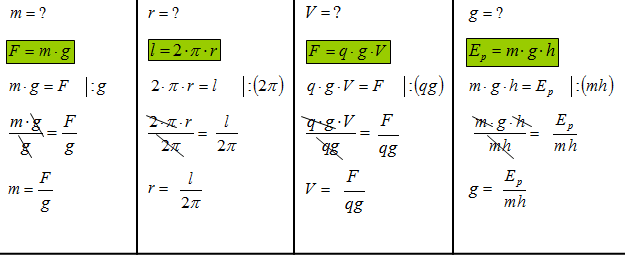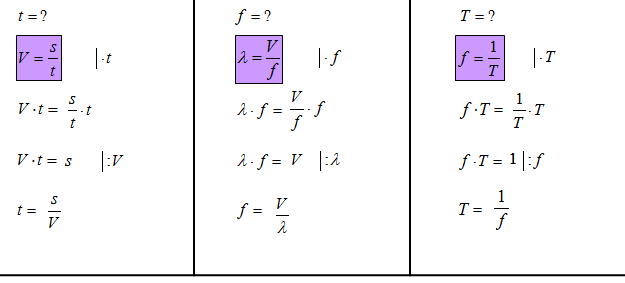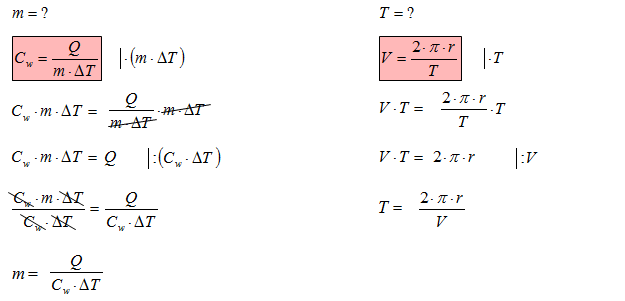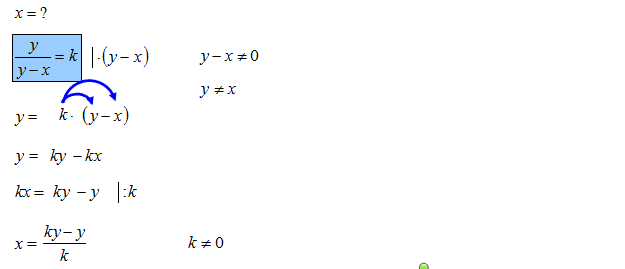Przekształcanie wzorów
Jak przekształcać wzory? Na początku przekształcania wzorów ciężko zauważyć, co trzeba najpierw zrobić?
Poznaj przepis na przekształcanie wzorów:
- Usuń mianownik – jeśli we wzorze są mianowniki warto całe równanie pomnożyć przez mianownik lub jeśli jest ich więcej przez wspólny mianownik występujących mianowników. Uwaga jeśli nie ma mianowników we wzorze przechodzisz do kolejnej instrukcji.
- Pomnóż przez nawias. Tutaj likwidujesz nawiasy wymnażając element stojący przed nawiasem przez elementy stojące w nawiasie. Uwaga: jeśli nie ma nawiasów pomijasz ten krok.
- Grupuj stronami. W tym kroku na lewą stronę przenosisz wszystkie elementy z niewiadomą (zazwyczaj są to x-sy), na prawą stronę przenosisz resztę elementów tzn. liczby i inne symbole. Redukujesz dalej pogrupowane jednomiany. Uwaga: jeśli elementy były już pogrupowane idziesz do punktu 4.
- Wyłącz wspólny czynnik przed nawias. Czasem są przykłady, które po redukcji mają z lewej strony dwa lub więcej elementów z niewiadomą i to właśnie tę niewiadoma należy wyłączyć z lewej strony wzoru. Zazwyczaj wyłączamy x przed nawias. Jeśli nie trzeba wyłączać przed nawias niewiadomej przechodzisz do punktu 5.
- W ostatnim kroku masz zazwyczaj symbol x z liczbą lub z innym symbolem, albo też z nawiasem. W takich sytuacjach chcąc pozbyć się tychże elementów dzielisz równanie przez element towarzyszący niewiadomej zazwyczaj jest to x.
Jak przekształcać wzory matematyczne i fizyczne? To proste, korzystam z podanego powyżej przepisu. Choć jak sam się przekonasz, nie jest to jedyny dobry sposób – są inne alternatywne, które też działają. Jeśli masz problem wykorzystaj ten przepis, a na pewno się nie zawiedziesz. Musisz wiedzieć, że w prostych przykładach wykorzystuje się jeden lub dwa punkty z wymienionej instrukcji, zaś trudniejsze przykłady wykorzystują cztery pierwsze kroki z przepisu.
Jak przekształcać wzory – zadania
Wyznacz wskazaną zmienną ze wzoru \(\frac{1}{f}=\frac{1}{x}+\frac{1}{y}\).
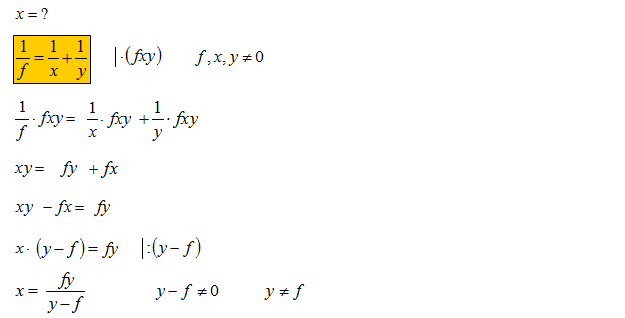
Wyznacz wskazaną zmienną ze wzoru \(2x=\frac{xy+2}{3}\).(Przekształcanie wzorów matematyka)
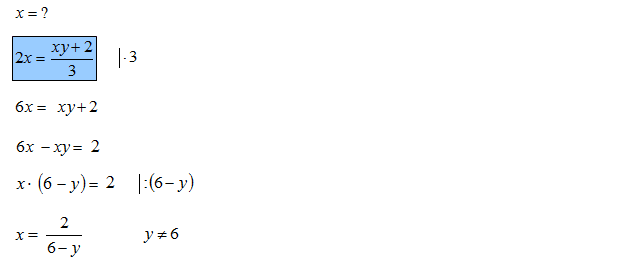
Wyznacz wskazaną zmienną x ze wzoru \(F=G\cdot \frac{M\cdot m}{{{r}^{2}}}\)
We wzorze na siłę grawitacji \({F_G} = G\frac{{{m_1} \cdot {m_2}}}{{{r^2}}}\) G jest stałą grawitacji, a poszczególne zmienne oznaczają odpowiednio: \({m_1},\,{m_2}\) – masy oddziaływujących grawitacyjnie ciał, r – odległość między środkami ciał.
- Wartość zmiennej r obliczymy ze wzoru postaci: \(r = \sqrt {\frac{{G\,{m_1}{m_2}}}{{{F_G}}}} \) PRAWDA/FAŁSZ
- Jeżeli masy ciał są równe, to wzór przyjmuje postać: \({F_G} = G\frac{{2m}}{{{r^2}}}\) PRAWDA/FAŁSZ
- Wartość siły grawitacji \({F_G}\) rośnie wraz z odległością r ciał. PRAWDA/FAŁSZ