Kurs: Potęgi i pierwiastki z egzaminów gimnazjalnych

Tylko sobie wyobraź: zamiast męczyć się z:
- Potęgami.
- Pierwiastkami.
- Zadaniami z treścią.
- Humorami nauczyciela matematyki.
- Nauką do egzaminu gimnazjanego.
…od dzisiaj raz na zawsze zapominasz o problemach związanych z potęgami i pierwiastkami.
Po szkole siadasz sobie wygodnie przed swoim komputerem i przez 30 minut dziennie oglądasz wideo korepetycje przygotowujące do egzaminu gimnazjalnego z matematyki.
Tego samego dnia uświadamiasz sobie, że uczysz się szybciej i umiesz więcej. Jesteś lepszym uczniem.
Jak to możliwe, że tak szybko opanujesz najważniejszy materiał do egzaminu gimnazjalnego?
- Uczysz się od doświadczonego korepetytora matematyki przy pomocy multimedialnych filmów.
- Poznajesz najważniejsze zadania do egzaminu gimnazjalnego, które mogą pojawić się na tegorocznym egzaminie gimnazjalnym.
- Wszystkie zadania omówione są maksymalnie szczegółowo, więc jeśli masz braki w matematyce, będzie to złoty środek.
- Brak presji czasowej – uczysz się wtedy, kiedy masz ochotę.
- Brak presji psychicznej – uczysz się sam, według wyznaczonego schematu.
Założę się, że Ty też popełniasz ten błąd w nauce do egzaminu
Większość uczniów do egzaminu gimnazjalnego z matematyki uczy się z książek i zeszytu. Jednak mało kto poznał zadania do egzaminów z poprzednich lat. To one są najlepszym drogowskazem prowadzącym do zaliczenia testu. Przetestuj swoją wiedzę z potęg i pierwiastków na podstawie zadań z egzaminów gimnazjalnych z poprzednich lat.
Nie wierzysz w pozytywny wynik na egzaminie?
Jeżeli masz znaczne luki w matematyce, otrzymujesz niezbęde materiały i szybko uzupełniasz braki. Moi uczniowe chcą efektów od zaraz, dlatego opracowałem skuteczny schemat przygotowania do egzaminu gimnazjalnego.
Jeżeli jesteś dobry z matematyki, od razu przechodzisz do właściwego programu nauczania.
Szybka i skuteczna nauka do egzaminu gimnazjalnego
Otrzymujesz potężną porcję matematycznej wiedzy zapakowanej w filmy wideo. Poznasz schematy zadań, jakie pojawiają się na egzaminach z matematyki i zobaczysz pewne prawidłowości, o których mało kto wie.

Marek Duda – matematyk i doświadczony korepetytor matematyki z ponad dziesięcioletnim stażem. Właściciel serwisu matematycznego – MatFiz24.pl. Jako jedyny w Polce nagrał odpowiedzi wideo do wszystkich egzaminów gimnazjalnych z matematyki i zapakował tutaj najlepszą porcję wiedzy, która z pewnością okaże się pomocna do zaliczenia egzaminu.
Nie odkładaj tego kursu na później
Zbiór zadań występujący poniżej to prawdziwy mix wiadomości o potęgach i pierwiastkach. Wykonaj samodzielnie zadania, zobacz rozwiązania wideo i zdaj bez problemu egzamin gimnazjalny z matematyki.
Na egzaminie gimnazjalnym z matematyki widać tendencję, że wśród zadań z potęgowania dość często występuje notacja wykładnicza.
Im wcześniej rozpoczniesz naukę przed egzaminami – tym lepszy wynik w końcowym rozrachunku!
Czy chcesz odwlekać naukę do egzaminu? Jaka jest Twoja decyzja?
Egzamin gimnazjalny 2015
Dane jest przybliżenie \(\sqrt{5}\approx 2,236.\)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
Rozwiązanie:
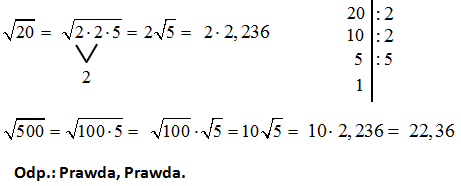
Poniżej podano kilka kolejnych potęg liczby 7.
71 = 7
72 = 49
73 = 343
74 = 2401
75 = 16 807
76 = 117 649
77 = 823 543
78 = 5 764 801
79 = 40 353 607
…………….
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Cyfrą jedności liczby 7190 jest
Rozwiązanie:
Należy zauważyć, ze ostatnie cyfry powtarzają się okresowo: 7,9,3,1,7,9,3,1,7,9,3,1,……itd. Zatem co czwarta potęga (ta z wykładnikiem podzielnym przez 4 ma na końcu cyfrę 1). Tym sposobem obliczamy 7188=…1, a kolejne potęgi powtarzają się w okresie 7,9,3,1. Dlatego 7189=…7, 7190=…9.
Odp.: D=9.
Egzamin gimnazjalny 2014
Dane są liczby: 3, 34, 312.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Iloczyn tych liczb jest równy
A. 316 B. 317 C. 348 D. 349
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
A. 10 i 11 B. 11 i 12 C. 12 i 20 D. 30 i 40
Egzamin gimnazjalny 2013
Dane są liczby: a = (–2)12, b = (–2)11, c = 210.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczby te uporządkowane od najmniejszej do największej to:
A. c, b, a. B. a, b, c. C. c, a, b. D. b, c, a.
Egzamin gimnazjalny 2012
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.

Egzamin gimnazjalny 2008
W różnych publikacjach jako jednostka energii pojawia się czasem toe. 1 toe odpowiada energii, jaką uzyskuje się z 1 tony ropy naftowej i równa się 41 868 MJ (1 MJ = 1 000 000 J). Ilu dżulom równa się 1 toe?
A. 4,1868 · 1011 B. 4,1868 · 108 C. 4,1868 · 109 D. 4,1868 · 1010
Egzamin gimnazjalny 2005
Średnia odległość Marsa od Słońca wynosi 2,28·108 km. Odległość ta zapisana bez użycia potęgi jest równa
A. 22 800 000 km
B. 228 000 000 km
C. 2 280 000 000 km
D. 22 800 000 000 km
Egzamin gimnazjalny 2003
1 mol to taka ilość materii, która zawiera w przybliżeniu 6·1023 (odpowiednio) atomów, cząsteczek lub jonów. Ile cząsteczek wody zawartych jest w 0,25 mola wody?
A. 1,5·1023 B. 0,5·1022 C. 1023 D. 0,25·1023- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
-
Kurs potęgowanie i pierwiastkowanie

- Co to jest potęga
- Potęgi – wzory
- Dodawanie i odejmowanie potęg o tych samych podstawach
- Mnożenie i dzielenie potęg o tych samych podstawach
- Potęga potęgi
- Potęga iloczynu i ilorazu
- Potęga o wykładniku całkowitym ujemnym
- Notacja wykładnicza
- Potęgi – zadania
- Potęgowanie – Sprawdzian
- Kurs: Potęgi i pierwiastki z egzaminów gimnazjalnych





