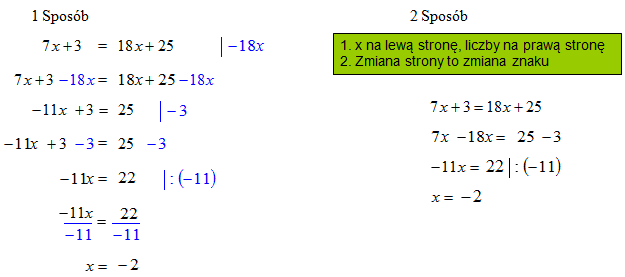Rozwiąż równanie
Równania liniowe mogą być omawiane w szkole podstawowej, gimnazjum i liceum. Rozwiązywanie równań nie jest najprostszym działem matematycznym, więc do dzieła…
W równaniach, w celu obliczenia niewiadomej „x” możesz wykonać dodawanie, odejmowanie, mnożenie i dzielenie stronami równania. Metoda dodawania stronami polega na dodaniu takiej liczby, czy symbolu do obu stron równania w celu jego uproszczenia.
Jak rozwiązywać równania liniowe?
Rozwiąż równanie: 3x – 5 = 2x – 7.
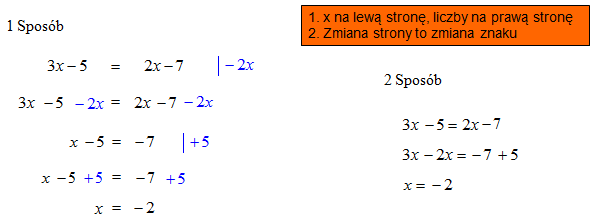
1 Sposób: jest dla początkujących. Zauważ, że rozwiązanie równania dąży do postaci np.: „x = 3”. Z lewej strony chcesz otrzymać „x”, a z prawej liczbę.
Elementy, które dodajesz stronami zaznaczono na równaniu kolorem niebieskim.
Likwidujesz „2x” z prawej strony. W tym celu możesz odjąć od obu stron równania „-2x”. Tym sposobem do obu stron równania dopisujesz wyrażenie „2x” otrzymując po redukcji wyrazów podobnych „x – 5 = -7”. Teraz zlikwiduj „-5” po lewej stronie. Możesz do obu stron dodać „+ 5” dzięki czemu redukujesz z lewej strony „-5”, a z prawej zmieni się wartość liczbowa. Otrzymujesz wynik: „x = -2”.
2 Sposób: jest szybszy i w zasadzie wynika z 1 sposobu.
Pierwsze zdanie w ramce: „x na lewą stronę, liczby na prawą stronę” informuje nas, że podczas rozwiązywania równania na początku grupujesz równanie stronami, x-sy przenosisz na lewą, a liczby na prawą stronę równania.
Drugie zdanie w ramce: „Zmiana strony to zmiana znaku” mówi Ci, że jeśli zmieniasz stronę elementu, to musisz zmienić też jego znak na przeciwny.
Rozwiąż równanie: \(\frac{4}{5}x+7=\frac{1}{3}x+10\)
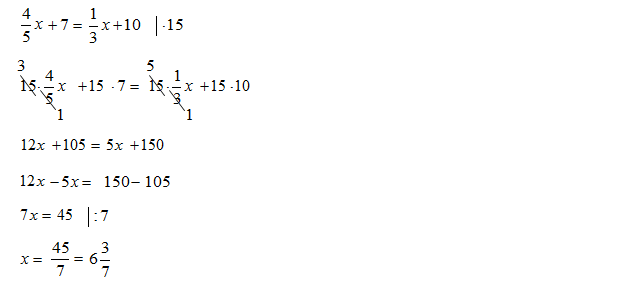
- 1 linijka: W przedstawionym zadaniu występują ułamki. Należy się ich pozbyć, aby obliczenia były prostsze. W tym celu całe równanie mnożysz przez liczbę, która jest wspólnym mianownikiem, mianowników występujących w równaniu. Tutaj w mianownikach jest „5” i „3” zatem na końcu równania dopisujemy pionową kreskę ze znakiem mnożenia: \(\mid \cdot 15\)
- 2 linijka: Całe równanie mnożymy przez „15”. Skracamy liczby.
- 3 linijka: Wymnażamy liczby.
- 4 linijka: Pogrupowaliśmy równanie stronami. Symbole przenosimy na lewą, a liczby na prawą stronę równania. Podczas takiego przenoszenia pamiętaj o zmianie znaku na przeciwny.
- 5 linijka: Redukujemy x-sy i liczby.
- 6 linijka: Otrzymujemy wynik. Staramy się zapisać go w jak najprostszej postaci.
Rozwiąż równanie: \(4\left ( x+1 \right )-3\left ( x-5 \right )=-13-3x\)

- 1 linijka: Zauważamy, że trzeba zlikwidować nawiasy.
- 2 linijka: Wymnażamy liczbę przez nawias tak jak pokazują strzałki.
- 3 linijka: Tutaj pogrupowaliśmy jednomiany z x-sami na lewą, a liczby na prawą stronę równania.
- 4 linijka: redukujemy wyrazy podobne, czyli x-sy z lewej, a liczby z prawej strony. Chcąc obliczyć „x”, musimy pozbyć się liczby „4”. W tym celu całe równanie dzielimy stronami przez „4”.
- 5 linijka: Otrzymujemy wynik.
Rozwiąż równanie: \[8\frac{1}{3}x+4\frac{1}{2}=7\frac{1}{2}x+3\frac{1}{3}\]
Uwaga: W tym zadaniu na początku zamień liczby na ułamki niewłaściwe. W dalszej kolejności usuń mianowniki mnożąc równanie przez wspólny mianownik liczby stojących w mianownikach.
Rozwiąż równanie: \[5\cdot \left ( \frac{1}{7}x-2 \right )-3\cdot \left ( \frac{1}{2}-x \right )=-4\frac{1}{14}\]
Tutaj na początku wymnóż liczby przez nawiasy, w kolejnym kroku usuń mianowniki, aby łatwiej się liczyło.