Wzór na przekątną kwadratu
Zobacz już teraz wzór na przekątną kwadratu:
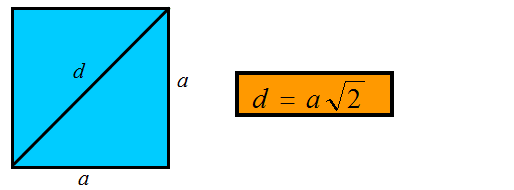
Przekątna kwadratu – wyprowadzenie wzoru
Wzór na przekątną kwadratu wyprowadza się z Twierdzenia Pitagorasa. Oznaczmy na rysunku boki kwadratu przez literkę „a”, zaś przekątną kwadratu literką „d”.
Dalej korzystamy z Twiedzenia Pitagorasa. Dodajemy z kwadratami przyprostokątne i otrzymana suma jest równa przeciwprostokątnej(przekątnej) podniesionej do kwadratu.
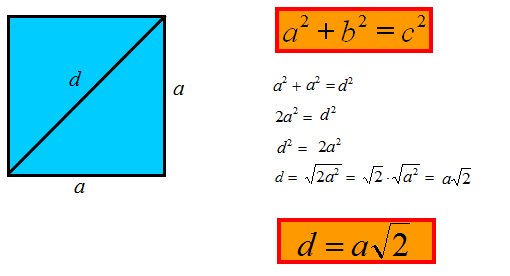
Jak obliczyć przekątną kwadratu?
Zastanawiasz się, jak w praktycznych zadaniach obliczyć przekątną kwadratu? Odpowiedź jest prosta – wykorzystując wzór na przekątną kwadratu…
Obliczenie przekątnej z Twierdzenia Pitagorasa jest metodą dłuższą i zwiększającą ilość błędów u niektórych uczniów. Dotyczy to szczególnie takich sytuacji, gdy uczeń otrzymuje liczbę pod pierwiastkiem i następnie wyłącza czynnik z pierwiastka – tutaj jest najwięcej problemów i błędów.
Wzór na przekątną kwadratu usprawnia i pomija niektóre obliczenia. Jest po prostu łatwiej i szybciej rozwiązywać zadania. Warto go zapamiętać!
Przekątna kwadratu – zadania
Obliczanie przekątnej kwadratu ze wzoru i z Twierdzenia Pitagorasa – porównanie metod.
Zadanie.
Oblicz przekątną kwadratu o boku 5cm ze wzoru, a następnie z Twierdzenia Pitagorasa. Porównaj szybkość obliczeń.
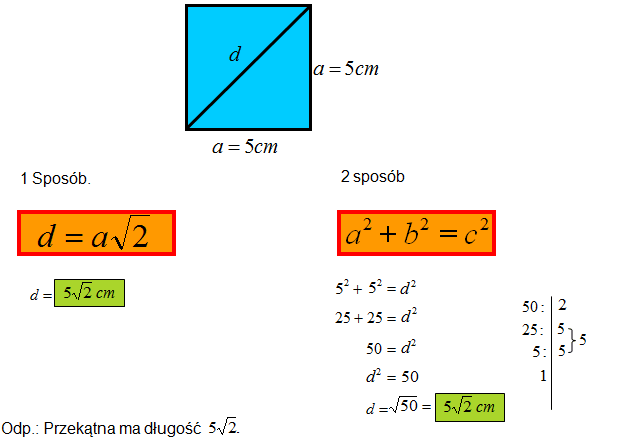
Widzisz, że jeśli zapamiętasz wzór na przekątną kwadratu, to podstawiając długość boku do wzoru automatycznie otrzymujesz wynik. W Twierdzeniu Pitagorasa trzeba wykonać kilka obliczeń.
Porównanie metod: Mając w pamięci wzór na przekątną kwadratu mamy 1 linijkę obliczeń. Obliczając przekątną z Twierdzenia Pitagorasa mamy 5 linijek oraz trudność z wyłączeniem czynnika przed znak pierwiastka.
Oblicz przekątną kwadratu o boku 8m. (Z Twierdzenia Pitagorasa i ze wzoru na przekątną).
Widzisz już, że obliczenia ze wzoru na przekątną kwadratu są znacznie szybsze w porównaniu z Twierdzeniem Pitagorasa.
Przekątna kwadratu jest o 1 dłuższa od bok tego kwadratu. Prawdą jest, że:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Przekątna kwadratu ma długość \(5\sqrt{2}\)cm. Pole tego kwadratu wynosi:
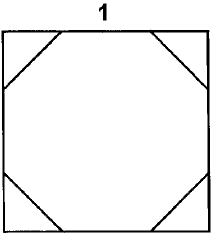
Z kwadratu wycięto ośmiokąt o boku 1 jak pokazano na rysunku.Oblicz pole tego ośmiokąta.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Suma długości boku kwadratu i jego przekątnej wynosi 1 dm.
- Pole tego kwadratu jest równe \(\frac{1}{3+2\sqrt{2}}d{{m}^{2}}.\) PRAWDA/FAŁSZ
- Obwód tego kwadratu wynosi \(\frac{4}{1+\sqrt{2}}dm. \) PRAWDA/FAŁSZ
- Przekątna tego kwadratu ma długość \(\frac{\sqrt{2}}{1+\sqrt{2}}dm. \) PRAWDA/FAŁSZ




