Pola figur podobnych – zadania

Mając dwa kwadraty, oblicz skalę podobieństwa mniejszego do większego.

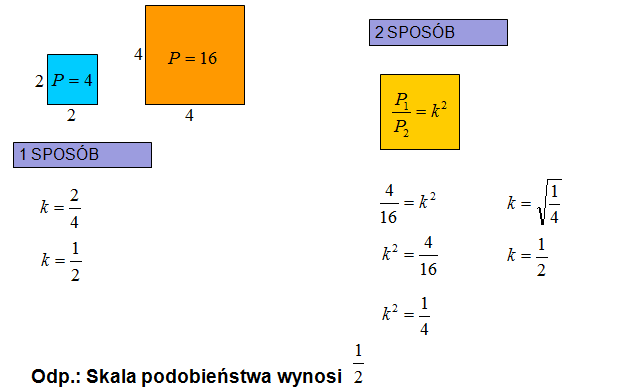
Zauważ, że mając dane boki i zarazem pola kwadratów można obliczyć skalę podobieństwa na 2 sposoby:

1 Sposób: Porównując bok mniejszego do boku większego kwadratu otrzymujesz skalę podobieństwa k = 1 : 2. Oczywiście możesz to zapisać w ułamku zwykłym, bądź dziesiętnym. W tym zadaniu jest to łatwiejszy sposób.

2 Sposób: Skalę podobieństwa można też obliczyć ze wzoru podanego wyżej w żółtej ramce.

Iloraz pól figur podobnych jest równy skali podobieństwa do kwadratu.

Obliczamy pole mniejszego kwadracika P = 4 oraz pole dużego kwadratu P = 16. Iloraz tych pól to 4/16, co po skróceniu daje 1/4. Powstały iloraz: jedna czarta jest równy skali podniesionej do kwadratu. Zatem, aby obliczyć skalę należy obliczyć pierwiastek ilorazu. W efekcie otrzymujesz skalę 1 : 2 (jedna druga).

Mając pola figur podobnych (P = 64cm², P = 1600mm²), oblicz skalę podobieństwa mniejszej figury do większej.

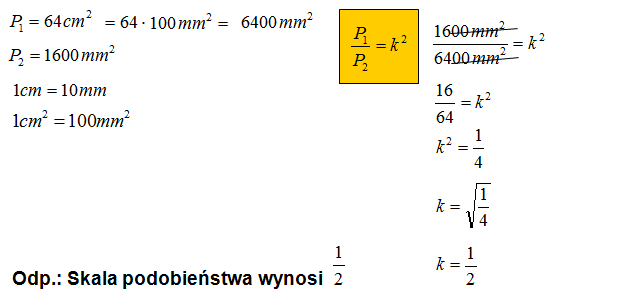
W tym zadaniu mamy dwie figury podobne o nieznanym kształcie. Porównując pola tych figur, obliczysz skalę podobieństwa do kwadratu. Usuwając kwadrat pierwiastkujesz równanie stronami. Pierwiastek z ilorazu pól będzie równy jedna druga 1 : 2.

Mając pola figur podobnych (P = 20cm², P = 10mm²), oblicz skalę podobieństwa mniejszej figury do większej.

Mieszkanie ma powierzchnię 80m², zaś na mapie ma powierzchnię 80cm². Oblicz w jakiej skali sporządzona jest ta mapa?

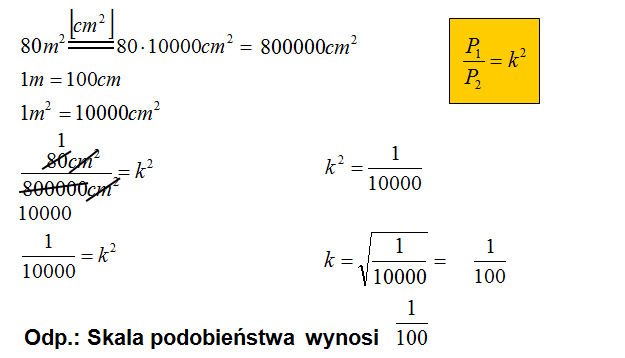
Na mapie w skali 1 : 1000 powierzchnia ma 2cm². Oblicz, ile arów i hektarów ma ta powierzchnia w rzeczywistości.

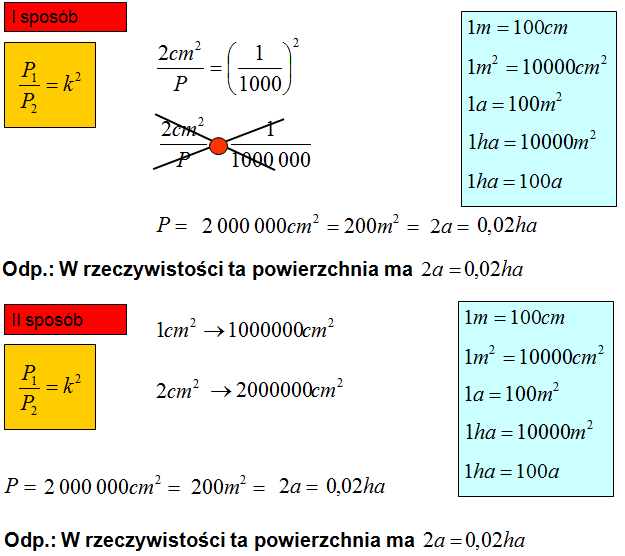
1 Sposób: Mając wzór w żółtej ramce na iloraz pól figur podobnych obliczamy skalę podobieństwa(więcej znajdziesz tutaj – https://matfiz24.pl/podobienstwo-figur. Wszystko polega na podstawieniu danych z zadania do wzoru. Dalej to tylko matematyczne przekształcenia.

Uwaga: Często uczniowie mimo, że znają prawidłowy wzór to podczas podstawiania zapominają dopisać kwadrat do skali podobieństwa. Pamiętaj o kwadracie przy skali!!!

2 Sposób: Skala podobieństwa 1 : 1000 informuje nas, że 1cm na mapie odpowiada 1000cm w rzeczywistości. Z tego wynika (po podniesieniu do kwadratu), że 1cm² na mapie odpowiada 1000000cm² w rzeczywistości. Wiedząc, że w zadaniu mamy 2cm², co odpowiada 2000000cm² w rzeczywistości.
Dalej to zamiana jednostek kwadratowych, ponieważ wynik rzeczywisty wyrażony w cm² jest dość niepraktyczny.

Na mapie w skali 1 : 10000 dany ogród zajmuje 5cm². Oblicz powierzchnię tego ogrodu w rzeczywistości.

Staw pan Andrzeja ma 50cm². Oblicz jaką zajmuje powierzchnię na mapie w skali 1 : 100?

1 Sposób: Mając pole w rzeczywistości i skalę podobieństwa bezpośrednio wstawiamy liczby do wzoru na iloraz pól kwadratów. Może na początku sprawić Ci problem, czy pole rzeczywiste wstawić do licznika, czy do mianownika? Otóż zerkasz na skalę i widzisz, że w mianowniku jest większa liczba, więc pole rzeczywiste wstawimy do mianownika, ponieważ odpowiada ono większej wartości ze skali podobieństwa. Mając już uzupełniony wzór z jedną niewiadomą, rozwiązujesz równanie.

Uwaga: Pamiętaj o kwadracie przy skali podobieństwa!!!

2 Sposób: Skala 1 : 100 mówi nam, że 1cm na mapie odpowiada 100cm w rzeczywistości. Jeśli podniesiesz skalę do kwadratu otrzymasz informację, że 1cm² na mapie odpowiada 10000cm² w rzeczywistości, a po zamianie jednostek otrzymujemy, że 1cm² na mapie odpowiada 1m² w rzeczywistości. Wobec tego 50cm² odpowiada 50m².