Cechy podobieństwa trójkątów
Cechy podobieństwa trójkątów są warunkami określającymi, kiedy trójkąty są podobne?
Mówiąc uproszczonym językiem figury podobne to takie, które mają taki sam kształt, lecz różnią się tylko skalą podobieństwa, czyli wielkością.
Pierwsza cecha podobieństwa trójkątów
Jeśli dwa trójkąty mają odpowiednie boki proporcjonalne to te trójkąty są podobne.
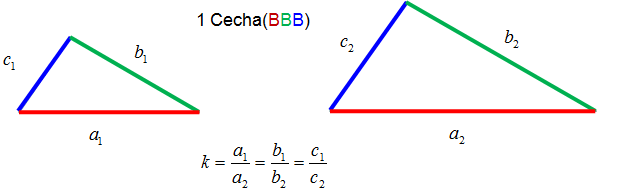
Możemy powiedzieć że trójkąty są podobne, jeśli narysowane są w pewnej skali jeden względem drugiego. Porównując odpowiednie boki:
- najkrótszy do najkrótszego
- średni do średniego
- najdłuższy do najdłuższego
otrzymujemy tę samą liczbę k – skalę podobieństwa.
Przykład.Sprawdź, czy podane trójkątny są podobne? Jeśli tak to podaj skalę podobieństwa.
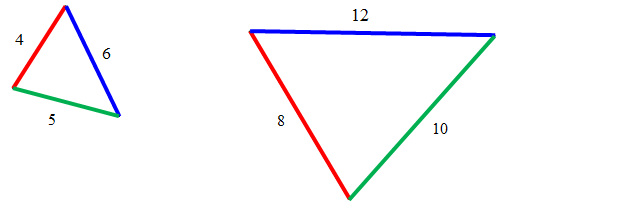
Porównujemy najkrótsze boki: \(\frac{4}{8}=\frac{1}{2}\)
Porównujemy średnie boki: \(\frac{5}{10}=\frac{1}{2}\)
Porównujemy najdłuższe boki:\(\frac{6}{12}=\frac{1}{2}\)
Druga cecha podobieństwa trójkątów
Jeśli dwa trójkąty mają taki sam kąt, a boki leżące na ramionach tego kąta są proporcjonalne, to te trójkąty są podobne.
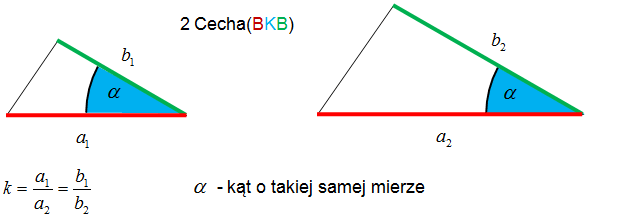 Przykład.
Przykład.Sprawdź, czy podane trójkątny są podobne? Jeśli tak to podaj skalę podobieństwa.

Porównujemy najkrótsze boki: \(\frac{2}{3}\)
Porównujemy średnie boki: \(\frac{3}{4,5}=\frac{30}{45}=\frac{2}{3}\)
Trzecia cecha podobieństwa trójkątów
Jeśli dwa trójkąty mają dwa takie same kąty, to te trójkąty są podobne.
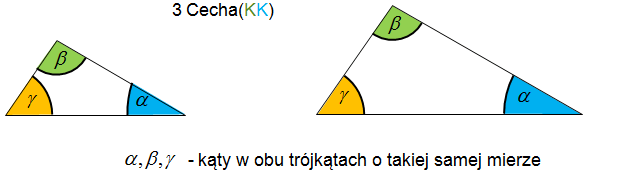
Zauważ, że z równości dwóch kątów w trójkątach wynika równość trzeciego kąta. Zatem możemy powiedzieć, że dwa trójkąty są podobne jeśli mają takie same kąty.
Przykład.Sprawdź, czy podane trójkątny są podobne?
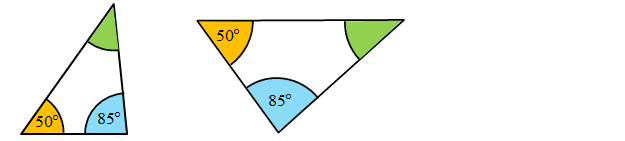
85°,50°- dwa kąty w obu trójkątach są identyczne, zatem pozostałe kąty (zielone) są sobie równe.




