Podobieństwo trójkątów
Można powiedzieć, że podobieństwo trójkątów oparte jest na:
- cechach przystawania trójkątów, czyli na własnościach określających, kiedy trójkąty są identyczne(przystające).
- cechach podobieństwa trójkątów, czyli własnościach informujących nas, kiedy jeden trójkąt został narysowany w pewnej skali względem drugiego trójkąta.
Podobieństwo trójkątów – zadania
Zobacz najważniejsze zadania do sprawdzianu w gimnazjum, które pozwolą Ci błyskawicznie przećwiczyć i opanować podobieństwo trójkątów.
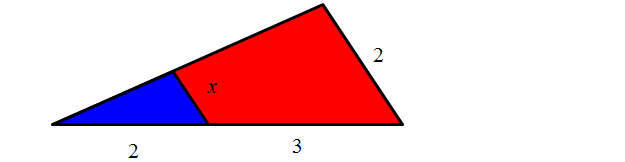
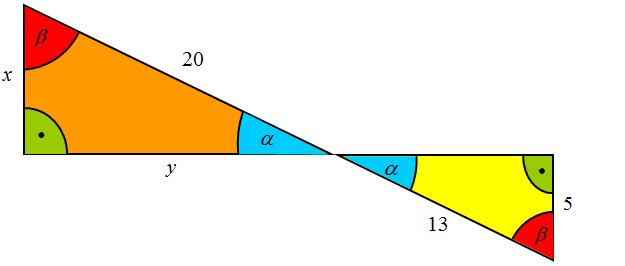
Jeżeli dwa trójkąty są podobne, to boki z pierwszego trójkąta są proporcjonalne do odpowiadających boków z drugiego trójkąta. Zbuduj proporcje (zależności) na podstawie rysunku.
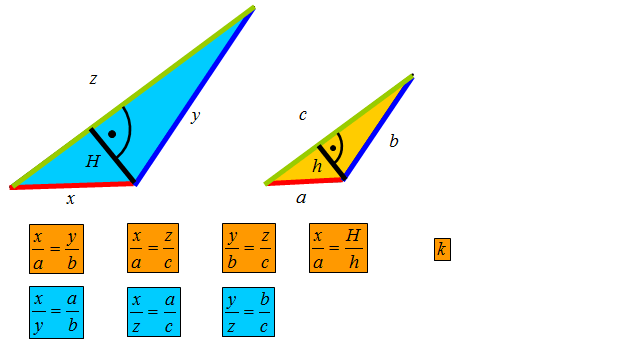
Pierwsze równanie powstaje przez porównanie ze sobą tych samych boków obu trójkątów. W pierwszym przypadku to czerwona podstawa dużego trójkąta x do czerwonej podstawy małego trójkąta a. Otrzymany iloraz jest skalą podobieństwa jednej figury do drugiej. Zatem iloraz x do a jest równy ilorazowi y do b. Bok y to prawy bok dużego trójkąta, a bok b to prawy bok mniejszego trójkąta.
Budując ilorazy zaznaczone na rysunku kolorem pomarańczowym, budujemy ilorazy będące skalą podobieństwa k.
Równania w niebieskich ramkach są również prawdziwe. Biorąc dwa boki z pierwszego dużego trójkąta, otrzymujemy iloraz równy ilorazowi dwóch odpowiadających boków z małego trójkąta.
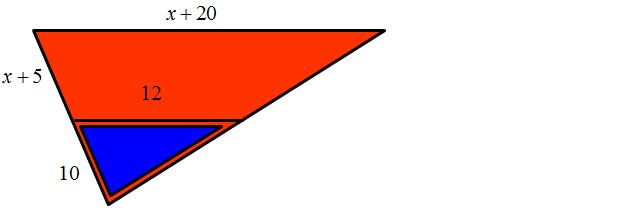
Wiedząc, że trójkąty są podobne oblicz bok o długości x.

Stosujemy tu podobieństwo figur. Iloraz dwóch boków z niebieskiego trójkąta (18 do x) jest równy ilorazowi odpowiadających boków z dużego czerwonego trójkąta (38 do 16).
Częstym błędem w tego typu proporcjach jest wzięcie liczby 20 do równania. Zauważ, że liczba 20 nie jest bokiem żadnego trójkąta, tylko trapezu. Budując równanie bierzesz oczywiście odpowiednie boki trójkątów.
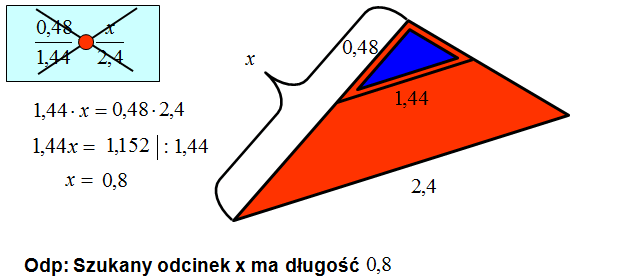
Wypisz podstawowe proporcje korzystając z rysunku opierając się na podobieństwie trójkątów lub wykorzystując Twierdzenie Talesa.
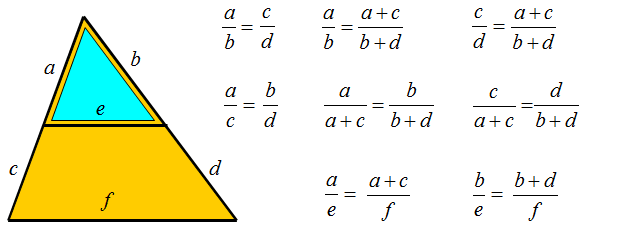
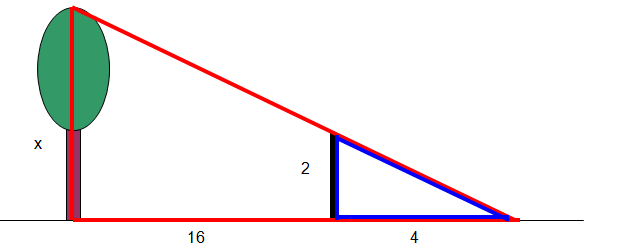
Oblicz wysokość budynku, jeśli masz dane zgodne z rysunkiem.
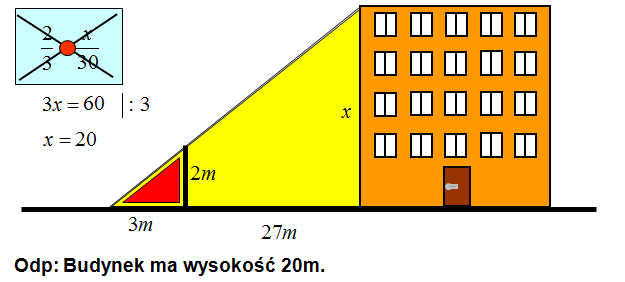
Można w dość łatwy sposób obliczyć wysokość budynku nie wspinając się po jego ścianach.
Można wbić w ziemię kij o znanej długości np. 2m. Następnie przesuwając głowę przy ziemi staramy się, aby nasze oko, koniec kija i wierzchołek budowli były w jednej linii.
Odległość okna od kija i odległość kija od budynku można zmierzyć taśmą mierniczą używaną na lekcjach wychowania fizycznego. W tym momencie otrzymujemy pomocniczy rysunek jak wyżej.
Zauważamy dwa trójkąty podobne. Jeden mały – zaznaczony kolorem czerwonym. Drugi duży – tu zakolorowany na żółto. Następnie budujesz pokazaną wyżej proporcję i rozwiązujesz ją mnożąc ją „po skosie”.
Człowiek o wysokości 1,5m rzuca cień o długości 4,5m. W tym samym czasie drzewo rzuca cień 45m. Oblicz wysokość drzewa.

Wiemy, że kąt padania promieni słonecznych jest taki sam dla człowieka jak i dla drzewa. Można więc tak ustawić kij, aby jego cień kończył się tam gdzie kończy się cień drzewa. W ten sposób otrzymujemy rysunek pokazany wyżej. Dalej korzystamy z podobieństwa trójkątów i budujemy proporcję wykorzystując odpowiadające przyprostokątne z jednego i drugiego trójkąta.
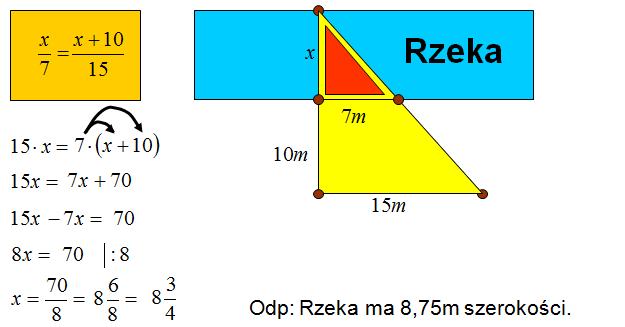
Oblicz szerokość rzeki mając następujący rysunek.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Rozsuwana drabina o długości 8m jest ustawiona do muru pod pewnym kątem sięga na wysokość 7m. O ile należy wydłużyć drabinę, aby sięgała na wysokość 10m (jeśli kąt nachylenia pozostaje stały).
Treść dostępna po opłaceniu abonamentu.W trójkącie równoramiennym ABC poprowadzono równoległy do podstawy |AB| odcinek |DF| = 5, którego końce znajdują się na ramionach tego trójkąta. Oblicz odcinek |AB| jeśli stosunek odcinka CD do DA jest równy 1 : 3.
Treść dostępna po opłaceniu abonamentu.W trójkącie ABC ramiona |AC| = |BC| = 16, podstawa |AB| = 18. Na ramieniu |AC| zaznaczono punkt X w odległości 4cm od wierzchołka trójkąta, zaś na ramieniu |BC| punkt Y tak, że odcinek |XY| jest równoległy do podstawy |AB|. Oblicz długość odcinka |XY|.
Treść dostępna po opłaceniu abonamentu.