Liczba odwrotna
Liczba odwrotna do danej liczby x, to taka liczba y, że xy=1. Zatem iloczyn liczby i liczby do niej odwrotnej daje wartość 1.
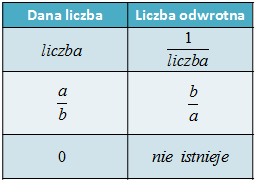
Liczba odwrotna w praktyce:
Jeśli chcesz wyznaczyć liczbę odwrotną do danej liczby to najpierw zapisz daną liczbę w postaci licznika i mianownika, a następnie wyznacz liczbę odwrotną zamieniając licznik z mianownikiem. Znaku nie zmieniaj. Osobiście przychodzi mi na myśl jakby liczba „stawała do góry nogami”.
Czy istnieje liczba odwrotna do 1? Odpowiedź: Liczbą odwrotną do 1 jest 1.
Czy istnieje liczba odwrotna do 2? Odpowiedź: Liczbą odwrotną do 2 jest \(\frac{1}{2}\).
Czy istnieje liczba odwrotna do 0 (zera)? Odpowiedź: Liczba odwrotna do zera nie istnieje.
Uwaga: Dlaczego nie ma liczby odwrotnej do zera?
Gdyby ktoś chciał utworzyć liczbę przeciwną do zera musiałby najpierw zero przedstawić w postaci ułamka zwykłego niewłaściwego postaci „licznik przez mianownik” np.0/2. Dalej należałoby zamienić miejscami licznik z mianownikiem i wówczas otrzymalibyśmy, że liczba przeciwna do zera jest równa 2/0. Wiemy jednak doskonale, że zero nie może być w mianowniku zatem jest to sytuacja niemożliwa. Stąd nie ma liczby odwrotnej do zera.
Ciekawostka:
Liczbą odwrotną do odwrotnej liczby x jest liczba x.
Dlaczego???
Wytłumaczenie ciekawostki:
Najpierw zastanów się jak wygląda odwrotna liczba do x? To liczba \(\frac{1}{x}\). Teraz obliczamy liczbę odwrotną do 1/x. Zatem należy zamienić licznik z mianownikiem i otrzymamy liczbę x.
liczba odwrotna – zadania standardowe
Znajdź liczbę odwrotną do danej liczby.
| Dana liczba | Liczba odwrotna |
| \(2=\frac{2}{1}\) | \(\frac{1}{2}\) |
| \(-5=-\frac{5}{1}\) | \(-\frac{1}{5}\) |
| \(-65=-\frac{65}{1}\) | \(-\frac{1}{65}\) |
| \(43=\frac{43}{1}\) | \(\frac{1}{43}\) |
| \(-\frac{2}{3}\) | \(-\frac{3}{2}\) |
| \(3\frac{1}{8}=\frac{25}{8}\) | \(\frac{8}{25}\) |
| 0 | nie istnieje |
| \(-2,45=-\frac{49}{20}\) | \(-\frac{20}{49}\) |
| \(0,32=\frac{8}{25}\) | \(\frac{25}{8}\) |
Rozwiązanie:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Podczas wyznaczania liczby odwrotnej otrzymujemy w mianowniku pierwiastek, wówczas pamiętaj, aby usunąć niewymierność z mianownika.
Liczba odwrotna – zadania trudne
Liczba x jest ułamkiem, którego licznik jest większy od mianownika o 3. Jeżeli licznik tego ułamka zwiększymy o 1, a mianownik zwiększymy o 10, to otrzymamy liczbę, która jest odwrotnością liczby x. Oblicz x.
Treść dostępna po opłaceniu abonamentu.Znajdź liczbę odwrotną do danej liczby.
| Dana liczba | Liczba odwrotna |
| \(\sqrt{5}\) | |
| \(\sqrt{3}-8\) | |
| \(7+\sqrt{2}\) |
Liczba \(\varphi =\frac{\sqrt{5}-1}{2}\) zwana jest liczbą złotą. Odwrotność ϕ, to:




