Konstrukcja odcinków niewymiernych- pierwiastek z liczby 5
Konstrukcja odcinków niewymiernych, a w tym przypadku pierwiastka z liczby 5 jest oparta na wiadomościach dotyczących Twierdzenia Pitagorasa.
Do znanego wzoru: \({{a}^{2}}+{{b}^{2}}={{c}^{2}}\) należy za jedną z literek a, b lub c wstawić pierwiastek z pięciu. Pozostałe literki trzeba uzupełnić liczbami naturalnymi, które trzeba wymyśleć lub trafić.
W efekcie otrzymujemy wzór: \({{1}^{2}}+{{2}^{2}}={{\sqrt{5}}^{2}}\)
Patrząc na niego widzimy, że \(\sqrt{5}\) jest przeciwprostokątną trójkąta prostokątnego o przyprostokątnych 1 i 2.
Jak narysować konstrukcję pierwiastka z liczby 5?
Krok 1
Znajdź dwie liczby naturalne, które wraz z \(\sqrt{5}\) będą spełniały wzór z Twierdzenia Pitagorasa
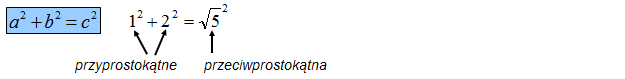
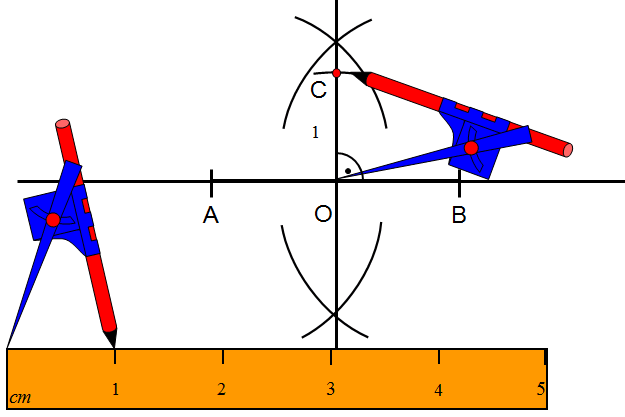
Krok 2
Budujesz odcinek na pewnej prostej

Krok 3
Rysujesz symetralną odcinka AB, otrzymując kąt prosty.

Krok 4
Na jednym z ramion otrzymanego kąta prostego odkładasz odcinek o długości 1cm. Otrzymałeś punkt C.
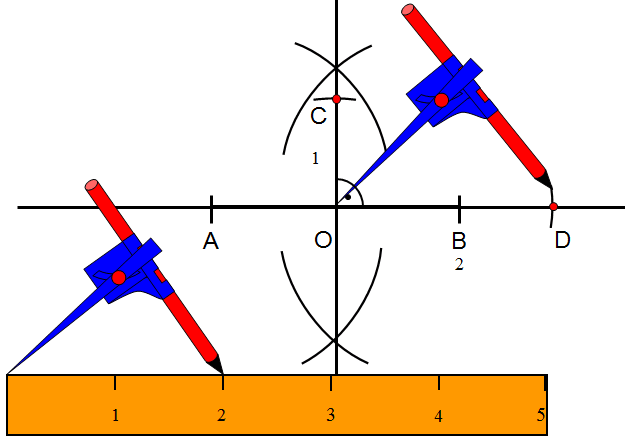
Krok 5
Na drugim ramieniu kąta prostego odkładasz odcinek o długości 2cm. Otrzymałeś punkt D.
Krok 6
Łączysz otrzymane punkty C i D przeciwprostokątną trójkąta OCD.
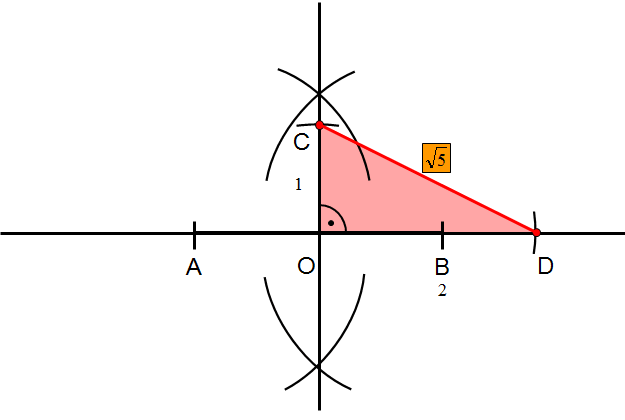
Na koniec warto się przyjrzeć, że konstrukcja pierwiastka z liczby jest oparta na trójkącie prostokątnym i na wzorze wynikającym z Twierdzenia Pitagorasa.




