Wzory skróconego mnożenia – Zadania i ćwiczenia
Poniżej przedstawiam najważniejsze wzory skróconego mnożenia. Ich znajomość na pewno przyda się podczas egzaminu gimnazjalnego i matury z matematyki!
\({{\left( a+b \right)}^{2}}={{a}^{2}}+2 a b+{{b}^{2}}\) – Kwadrat sumy dwóch wyrażeń
\({\left( {a – b} \right)^2} = {a^2} – 2 a b + {b^2}\) – Kwadrat różnicy dwóch wyrażeń
\(\left( {a + b} \right) \cdot \left( {a – b} \right) = {a^2} – {b^2}\) – Różnica kwadratów dwóch wyrażeń
\({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\) – Sześcian sumy dwóch wyrażeń
\({\left( {a – b} \right)^{\;3}} = {a^3} – 3{a^2}b + 3a{b^2} – {b^3}\) – Sześcian różnicy dwóch wyrażeń
\({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} – ab + {b^2}} \right)\) – Suma sześcianów
\({a^3} – {b^3} = \left( {a – b} \right)\left( {{a^2} + ab + {b^2}} \right)\) – Różnica sześcianów
\({\left( {a + b} \right)^n} = \left( {\begin{array}{*{20}{c}}
n\\
0
\end{array}} \right){a^n} + \left( {\begin{array}{*{20}{c}}
n\\
1
\end{array}} \right){a^{n – 1}}b + … + \left( {\begin{array}{*{20}{c}}
n\\
{n – 1}
\end{array}} \right)a{b^{n – 1}} + \left( {\begin{array}{*{20}{c}}
n\\
n
\end{array}} \right){b^n}\)
n -ta potęga sumy dwóch wyrażeń, inaczej dwumian Newtona
, gdzie \(\left( {\begin{array}{*{20}{c}}
n\\
k
\end{array}} \right) = \frac{{n!}}{{k!\left( {n – k} \right)!}}\) – symbol Newtona
Trójkąt Pascala
Współczynniki we wzorach skróconego mnożenia możesz również wyznaczyć z „trójkąta Pascala”.
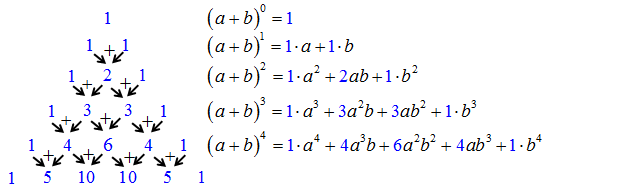 Zauważ, że wierzchołek i boczne krawędzie tego trójkąta stanowią liczby „1”. Wewnętrzne liczby powstają przez dodanie dwóch liczb znajdujących się w górnym wierszu.
Zauważ, że wierzchołek i boczne krawędzie tego trójkąta stanowią liczby „1”. Wewnętrzne liczby powstają przez dodanie dwóch liczb znajdujących się w górnym wierszu.
Przykładowe zadania ze wzorami skróconego mnożenia – rozwiązania
Uprość wyrażenie korzystając ze wzorów skróconego mnożenia.

Wzór skróconego mnożenia podany wyżej to tzw. kwadrat sumy.
Pierwszy element został umieszczony w zielonym kubku, drugi w czerwonym. W celu wykorzystania wzoru skróconego mnożenia podanego w żółtej ramce musisz pierwszy element „x” podnieść do kwadratu. Następnie dodajesz do niego podwojony iloczyn pierwszego i drugiego elementu. Na koniec dodajesz kwadrat ostatniego elementu z nawiasu, czyli podnosisz liczbę „1” do kwadratu. W kolejnym kroku należy ewentualnie zredukować lub wymnożyć wyrażenia algebraiczne.
Z czasem wiele redukcji będziesz robić automatycznie w pamięci.
Uwaga: W tym lub innych przykładach możesz ominąć wzory skróconego mnożenia. W tym celu można kwadrat sumy rozpisać na dwa nawiasy i wymnożyć je ze sobą według zasady każdy z każdym. Zobacz: „Mnożenie sum algebraicznych”. (tu link do nadrzędnej strony: Mnożenie sum algebraicznych).
Oblicz korzystając ze wzoru skróconego mnożenia.
\[{\left( {2x + 7} \right)^{\;2}} = \]Pewnie zauważyłeś, że zapis wzoru skróconego mnożenia zaczyna się podniesieniem do kwadratu pierwszego elementu: „2x”. W efekcie otrzymamy 4x2. Dalej myślę, że dasz radę. Jeśli nie, obejrzyj raz lub dwa film edukacyjny.
Oblicz kwadrat sumy dwóch jednomianów.
\[{\left( {\sqrt 3 + 3y} \right)^{\;2}} = \]W tym filmie należy zauważyć, że podnosząc pierwszy jednomian do kwadratu możesz skorzystać z własności pierwiastka podniesionego do potęgi. Kwadrat likwiduje pierwiastek i otrzymujemy w efekcie samą liczbę „3”. Pozostałe obliczenia tłumaczę na filmie.
Uprość wyrażenie korzystając ze wzorów skróconego mnożenia.
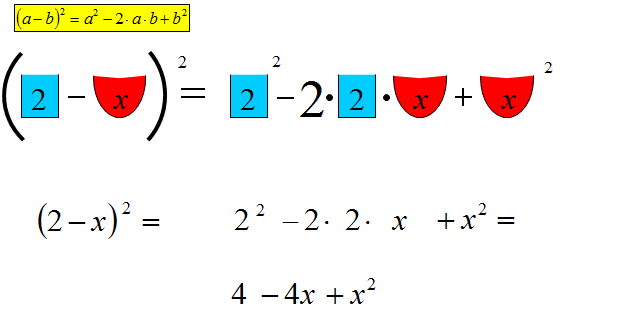
Wzory skróconego mnożenia są bardzo pomocne. W powyższym przykładzie pokazuję jak obliczyć kwadrat różnicy dwóch wyrażeń.
Pierwszy element został zaznaczony na niebiesko, drugi na czerwono. Patrząc na wzór w żółtej ramce podnosimy najpierw pierwszy jednomian „2” do kwadratu. Dalej odejmujemy podwojony iloczyn pierwszego jednomianu przez drugi. Na koniec dodajemy kwadrat ostatniego jednomianu.
Na początku warto dokładnie rozpisać wzór skróconego mnożenia. Z czasem pewne redukcje będziesz robić w pamięci. Powodzenia.
Oblicz wyrażenie algebraiczne wykorzystując wzór skróconego mnożenia.
\[{\left( {4x – 3} \right)^{\;2}} = \]Oblicz ze wzoru skróconego mnożenia.
\[{\left( {3x{y^3} – 2x} \right)^{\;2}} = \]W tym przykładzie pamiętaj, że jednomian \( 3x{y^3} \) traktujemy jako pierwszy element oznaczony we wzorze skróconego mnożenia: \({\left( {a – b} \right)^2} = {a^2} – 2 \cdot a \cdot b + {b^2}\) symbolem „a”. Na początku wzoru skróconego mnożenia jednomian \( 3x{y^3} \) podnosisz do kwadratu otrzymując: \({{\left( 3x{{y}^{3}} \right)}^{2}}\). Możesz tutaj skorzystać z własności potęgi iloczynu.
W kolejnym kroku odejmujesz podwojony iloczyn pierwszego elementu razy drugi element: \(-2\cdot 3x{{y}^{3}}\cdot 2x\).
Następnie zgodnie ze wzorem skróconego mnożenia dodajesz ostatni element z nawiasu podniesiony do kwadratu: \({{\left( 2x \right)}^{2}}\)
Na końcu wyrażenie algebraiczne możesz troszeczkę uprościć. Wymnażasz i podnosisz do potęgi.
Wymnóż nawiasy.
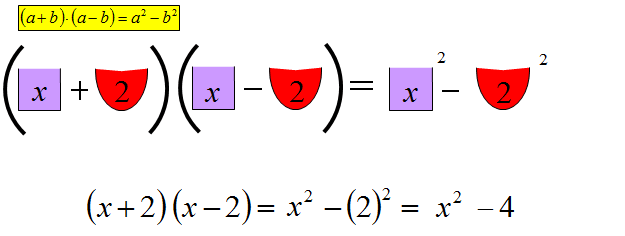
Powyższy przykład możesz rozwiązać wymnażając nawiasy przez siebie. Jednak lepszą metodą będzie zastosowanie wzoru skróconego mnożenia. Warto zapamiętać, że jeśli wymnażasz dwa nawiasy, które różnią się tylko wewnętrznymi znakami, wówczas wynikiem jest różnica kwadratów jednomianów występujących w nawiasach.
Wymnóż nawiasy.
\[\left( {3 + \sqrt 2 } \right)\;\left( {3 – \sqrt 2 } \right) = \]Wymnóż nawiasy.
\[\left( {x + 4y} \right)\;\left( {x – 4y} \right) = \]Zamień wyrażenie algebraiczne na postać iloczynową.
\[{x^2} – 9 = \] \[36 – 4{x^2} = \] \[61 – 2{x^2} = \] \[36{x^2} + 84x + 49 = \] \[{x^2} + 4x + 4 = \] \[\frac{1}{9}{x^2} – \frac{1}{3}xy + \frac{1}{4}{y^2} = \]W tym zadaniu wzory skróconego mnożenia odgrywają kluczową rolę. Chcąc zamienić wyrażenie na postać iloczynową w trzech pierwszych przykładach stosujemy wzór: \[\left( {a + b} \right)\left( {a – b} \right) = {a^2} – {b^2}\] W pierwszym przykładzie zauważasz, że masz tak na prawdę różnice dwóch kwadratów, bo \({x^2} – 9 ={x^2} – {3^2} \) stąd już dość prosto zauważyć, ze można tę różnicę rozpisać na dwa nawiasy, na postać iloczynową \({x^2} – {3^2} = \left( {x + 3} \right)\left( {x – 3} \right)\)
Ostatnie trzy przykłady wykorzystują wzór na kwadrat sumy, bądź różnicy. Spójrz na przykład \(36{x^2} + 84x + 49 \). Zauważasz, że pierwszy i ostatni jednomian to dwa kwadraty \({\left( {6x} \right)^2}\) oraz \({7^2}\), a środkowy jednomian jest podwojonym iloczynem pierwszego jednomianu przez drugi. Na tej podstawie w 4 i 5 przykładzie wykorzystujesz wzór: \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\), zaś w ostatnim przykładzie \[{\left( {a – b} \right)^2} = {a^2} – 2ab + {b^2}\]
Cały problem w tym zadaniu polega na zauważeniu, że nasze przykłady to prawa strona rozpisanego wzory skróconego mnożenia.
Skup się na znalezieniu dwóch kwadratów. Gdy je znajdziesz – pierwiastkuj je. Otrzymasz wówczas pierwszy i ostatni jednomian wzoru skróconego mnożenia.
Doprowadź wyrażenie algebraiczne do najprostszej postaci korzystając ze wzorów skróconego mnożenia.
\[{(2x – 0,2)^2} + (x – 0,1)(0,1 + x) = \] \[(2x – 1)(1 + 2x) – {(\sqrt 2 – 3{x^2})^2} = \]Doprowadź wyrażenie algebraiczne do najprostszej postaci korzystając ze wzorów skróconego mnożenia.
\[ – 4(x – 2) + {(x + 5)^2} + (x – 3)(x + 3) = \] \[{(2x – y)^2} – (x – y)(x + y) – 3{(x + 2y)^2} = \]Doprowadź wyrażenie algebraiczne do najprostszej postaci korzystając ze wzorów skróconego mnożenia.
\[{({x^{n + 1}} + 1)^{\;2}} = \] \[{(0,1{x^2} – {x^{1 – n}})^2} = \]Przed zastosowaniem wzoru skróconego mnożenia przypomnij sobie potęgę iloczynu i ilorazu.
Doprowadź wyrażenie algebraiczne do najprostszej postaci korzystając ze wzorów skróconego mnożenia.
\[{\left( {\frac{1}{6}{x^{3n + 1}} \cdot {y^{n + 2}} + \frac{6}{5}{y^{5n}} \cdot {x^{1 – n}}} \right)^2} = \]W tym zadaniu zasadniczą trudnością jest zauważenie dwóch rozbudowanych jednomianów wewnątrz nawiasów. Dalej stosujesz wzór skróconego mnożenia \[{\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\] Warto przypomnieć sobie tutaj jak potęgujemy jednomiany.
Uprość wyrażenie algebraiczne wykorzystując wzory skróconego mnożenia.
\[{(8x – 4y)^2} – 6x(x – y) + 2(x – 1)(x + 1) = \] \[8{\left( {x – \frac{1}{2}} \right)^2} – 5{\left( {x + \frac{1}{5}} \right)^2} + (3 – x)(x + 3) = \]- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Wartość wyrażenia (x+1)2-(2x+0,5)2 wynosi 0 dla:
Wzory skróconego mnożenia zadania bardzo trudne
Oblicz wartość wyrażenia \(\frac{a+b}{a-b}\) jeśli 0<b<a i a2+b2=4ab.
Wskazówka: wykorzystaj wzory skróconego mnożenia. Treść dostępna po opłaceniu abonamentu.Udowodnij, że wyrażenie a16-1 jest podzielne przez (a+1).
Treść dostępna po opłaceniu abonamentu.Udowodnij, że wyrażenie \(({3^{16}} – {1^{16}}) \) jest podzielne przez 40.
Treść dostępna po opłaceniu abonamentu.Udowodnij, że wyrażenie \({x^8} – {y^8}\) jest podzielne przez (x+y).
Treść dostępna po opłaceniu abonamentu.Jeżeli \(x+\frac{1}{x}=7\) i x≠0 , to wartość wyrażenia \({{x}^{2}}+\frac{1}{{{x}^{2}}}:\)
Różnica kwadratów dwóch
- kolejnych liczb całkowitych jest liczbą nieparzystą. PRAWDA/FAŁSZ
- kolejnych liczb naturalnych nieparzystych jest podzielna przez 8. PRAWDA/FAŁSZ
- liczb całkowitych różniących się o 2 jest liczbą podzielną przez 4. PRAWDA/FAŁSZ
- Zapisywanie wyrażeń algebraicznych
- Porządkowanie jednomianów
- Oblicz wartość liczbową wyrażenia
- Redukcja wyrazów podobnych
- Wyłączanie wspólnego czynnika przed nawias
- Mnożenie sum algebraicznych
- Wzory skróconego mnożenia
- Wyrażenia algebriaczne – sprawdzian
- Kurs: Wyrażenia algebraiczne z egzaminów gimnazjalnych




