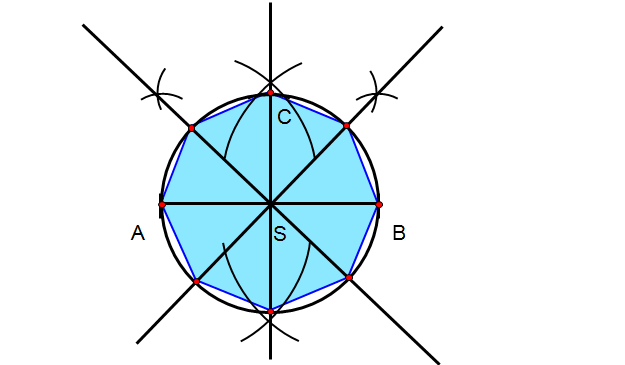
Konstrukcja ośmiokąta foremnego
Konstrukcja ośmiokąta foremnego – skrócony opis.
Do narysowania ośmiokąta foremnego należy dokładnie poznać dwie inne konstrukcje:
W skrócie konstrukcja polega na narysowaniu dwóch prostych (lub odcinków) przecinających się pod kątem prostym. Następnie kąty proste dzielisz na pół wykorzystując konstrukcję dwusiecznej kąta. Dalej ze środka przecięcia się prostych (lub odcinków) rysujesz okrąg, który przecina proste (lub odcinki) w punktach, które są wierzchołkami ośmiokąta foremnego.
Jak narysować ośmiokąt foremny – pełny opis konstrukcji
Krok 1
W celu narysowania konstrukcji ośmiokąta foremnego narysuj odcinek o końcach A i B. Dowolną rozwartością cyrkla większą od połowy danego odcinka z punktu A rysujesz łuk na górze i dole odcinka.
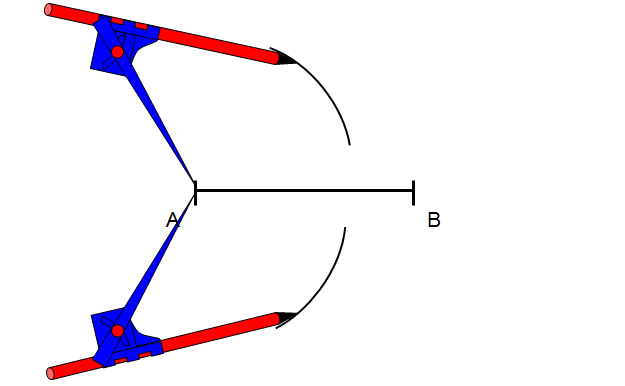
Krok 2
Nie zmieniając rozwartości cyrkla należy przejść do punktu B i również wykreślić łuki nad i pod odcinkiem. Wykonane łuki w tym i poprzednim kroku muszą się przeciąć!
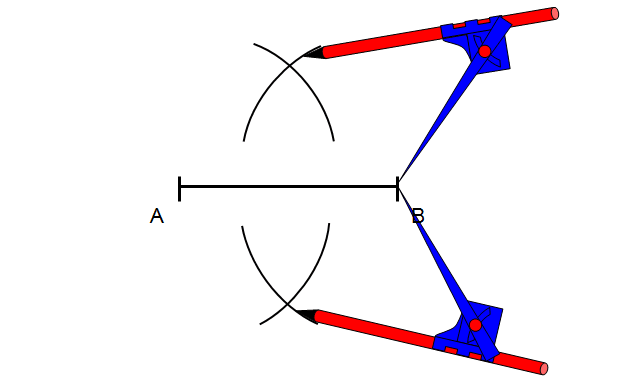
Krok 3
Punkty przecięcia się łuków należy połączyć prostą symetralną, która przechodzi dokładnie przez środek odcinka AB. Środek odcinka oznaczymy punktem S.
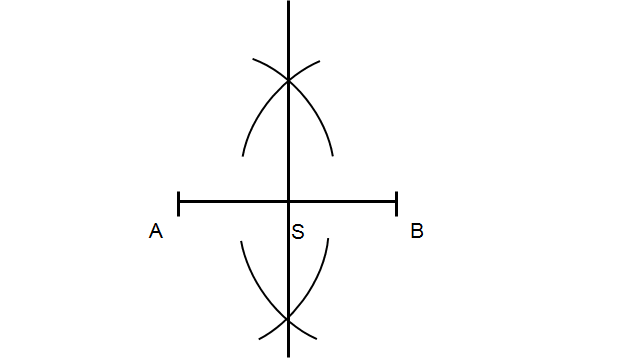
Krok 4
Wbij nóżkę cyrkla w punkt S. Odmierz cyrklem połowę odcinka AB (1) i zaznacz otrzymaną odległość na prostej symetralnej w punkcie C (2).
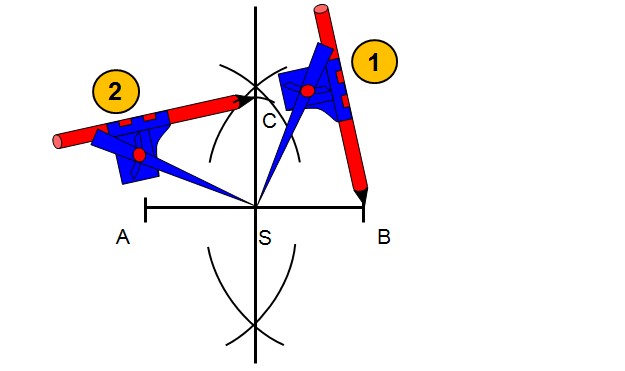
Krok 5
Nie zmieniając rozwartości cyrkla(połowa odcinka AB) przejdź do punktu B i wykonaj łuk na górze odcinka. Przejdź do punktu C i tą samą rozwartością cyrkla wykonaj łuk tak, aby otrzymane w tym kroku łuki przecięły się w jednym punkcie.

Krok 6
Punkt przecięcia otrzymanych łuków łączymy prostą przechodzącą przez środek odcinka AB. W ten sposób wyznaczyliśmy konstrukcyjnie dwusieczną kąta(podział kąta na pół).

Krok 7
Mając na cyrklu odmierzoną odległość równą połowie odcinka AB, przechodzisz do punktu A i wykonujesz łuk na górze odcinka. Przejdź teraz do punktu C i wykonaj łuk tak, aby nastąpiło przecięcie krzywych.
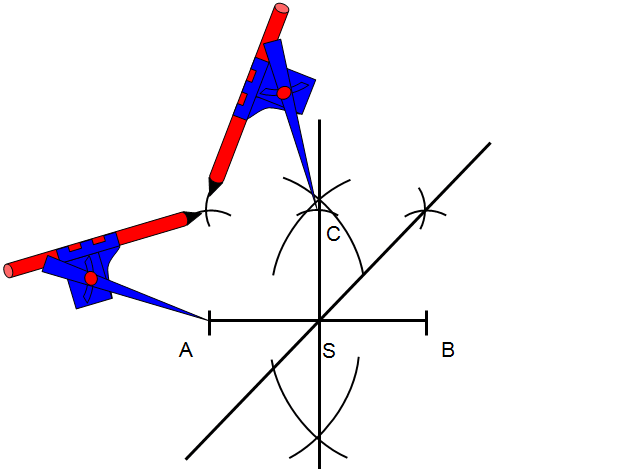
Krok 8
Punkt przecięcia łuków połącz prostą ze środkiem odcinka AB. Po raz kolejny wykonaliśmy konstrukcję dwusiecznej kąta.
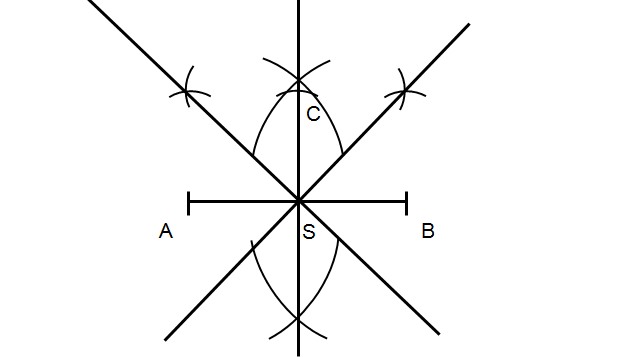
Krok 9
Z puntu S odmierz cyrklem odległość do punktu C, a następnie wykonaj okrąg. Zauważ, że promień tego okręgu jest równy połowie odcinka AB! Zwróć uwagę, że otrzymaliśmy 8 punktów na rysunku zaznaczonych kolorem czerwonym.
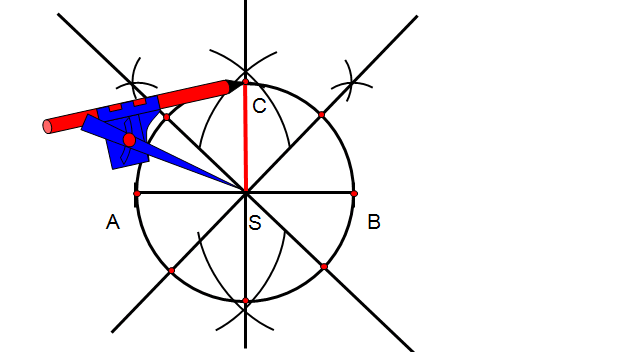
Krok 10
Otrzymane punkty z przecięcia okręgu należy połączyć otrzymując ukończoną konstrukcję ośmiokąta foremnego.