Suma ciągu arytmetycznego
Wyznacz sumę 20 początkowych wyrazów ciągu arytmetycznego (an) wiedząc, że pierwszy wyraz tego ciągu wynosi 7, zaś różnica ciągu arytmetycznego to liczba 4.
Propozycja rozwiązania:

2 Sposób:
Można też wykonać to zadanie wykorzystując drugi wzór na sumę ciągu arytmetycznego:
\(\begin{align}
& {{S}_{n}}=\frac{2{{a}_{1}}+\left( n-1 \right)\cdot r}{2}\cdot n \\
& {{S}_{20}}=\frac{2{{a}_{1}}+19\cdot r}{2}\cdot 20 \\
& {{S}_{20}}=\frac{2\cdot 7+19\cdot 4}{2}\cdot 20 \\
& {{S}_{20}}=900 \\
\end{align}\)
Wyznacz sumę wszystkich liczb trzycyfrowych.
Propozycja rozwiązania
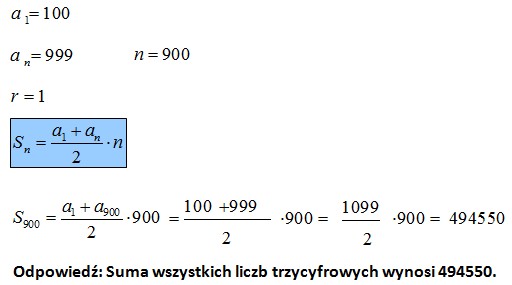
W tym zadaniu mamy pierwszy i ostatni wyraz ciągu arytmetycznego. Szukamy sumy liczb trzycyfrowych zatem najmniejszą liczbą 3-cyfrową jest liczba 100, zaś największą to 999. To proste. Można natomiast popełnić błąd licząc ile jest liczb trzycyfrowych.
Weźmy przykład: „Ile jest liczb od 10 do 19?”
Odpowiedź: 10, ponieważ mamy liczbę 10 oraz od 11 do 19 jest 9 liczb.
Powracając do głównego zadania jest 900 liczb trzycyfrowych, ponieważ mamy jedną liczbę 100 oraz od liczby 101 do 999 jest 899 liczb. Łącznie 900 liczb 3-cyfrowych. W tym momencie mamy wszystkie wielkości, które należy wstawić do wzoru na sumę ciągu arytmetycznego.
Wiedząc, że ciąg jest arytmetyczny oraz pierwszy wyraz ciągu jest równy 3, a jego różnica wynosi 2, wyznacz trzydziesty wyraz ciągu oraz sumę 30 pierwszych wyrazów tego ciągu.
Propozycja rozwiązania:
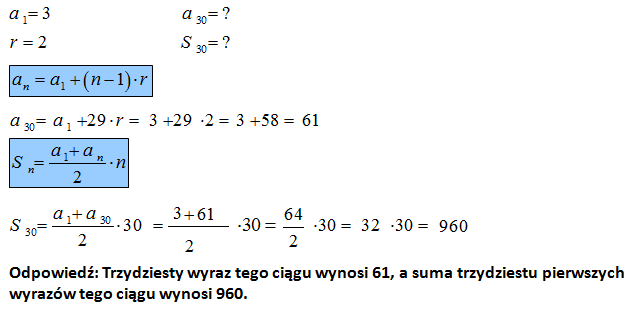
Ciąg (an) jest arytmetyczny oraz pierwszy wyraz tego ciągu wynosi 4, zaś jego różnica (-0,5). Jeden z jego wyrazów wynosi (-1). Wyznacz, który to wyraz ciągu oraz oblicz sumę od pierwszego do wyznaczonego wyrazu ciągu.
Propozycja rozwiązania:

Mając a1-pierwszy wyraz ciągu, r-różnicę, oraz n-ty wyraz an można podane wartości liczbowe wstawić do wzoru na n-ty wyraz ciągu arytmetycznego i obliczyć n=11, czyli ilość wyrazów potrzebną do obliczenia sumy. Automatycznie otrzymujemy również informację, że jeśli an=-1, to a11=-1, ponieważ n=11. W dalszej kolejności obliczenie sumy jest już tylko formalnością.
W ciągu arytmetycznym trzeci wyraz ciągu wynosi 1,8, zaś jego różnica 0,4. Ile wyrazów tego ciągu daje sumę równą 204?
Propozycja rozwiązania
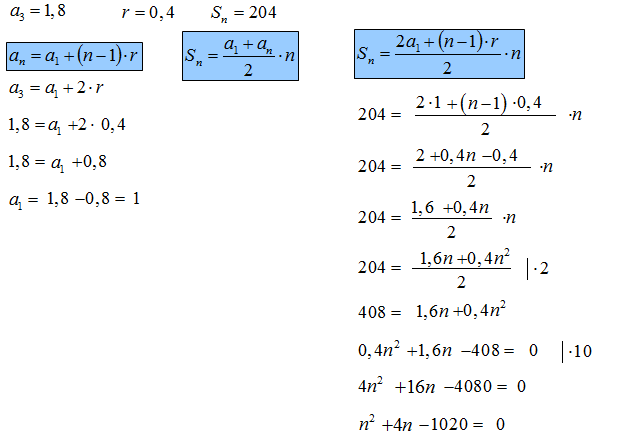 Dalej rozwiązujemy równanie kwadratowe:
Dalej rozwiązujemy równanie kwadratowe:
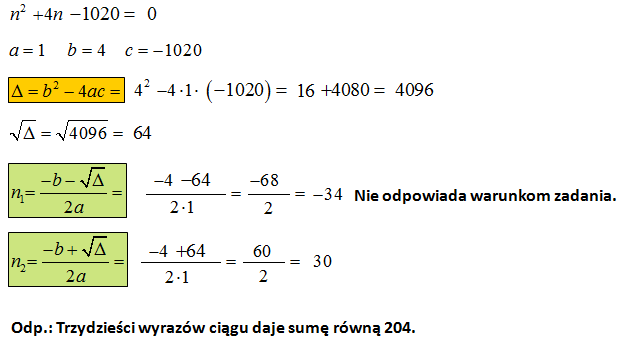
Dany jest ciąg arytmetyczny (an), w którym pierwszy wyraz ciągu to liczba 120. Oblicz jego setny wyraz oraz jego różnicę, jeśli suma stu początkowych wyrazów tego ciągu wynosi (-12750).
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Wyznacz x, czyli rozwiąż równanie: 1+4+7+10+14+…+x=3725 wiedząc, że składniki sumy lewej strony równania są kolejnymi wyrazami ciągu arytmetycznego (an).
Treść dostępna po opłaceniu abonamentu.



