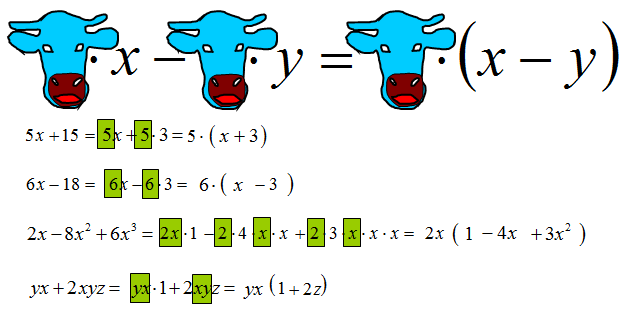Wyłączanie wspólnego czynnika przed nawias
Wyłączanie wspólnego czynnika przed nawias polega na zauważeniu w sumie algebraicznej takich samych elementów, które budują jednomiany.
Spójrz na przykład, w którym występuje krowa. W każdym z czynników występuje w iloczynie rysunek krowy, który może być zastąpiony dowolnym wyrażeniem algebraicznym. W tym przykładzie możesz wyłączyć przed nawias czynnik powtarzający się w obu jednomianach. Powtarza się tutaj krowa, więc wyłączymy głowę krowy przed nawias.
Teraz zastanawiasz się co będzie w nawiasie. Jedno z prostszych tłumaczeń głosi, że w nawiasie będzie wynik dzielenia Twojego przykładu przez wyłączony czynnik.
Inne tłumaczenie głosi, że po wyłączeniu czynnika przed znak pierwiastka zastanawiasz się co trzeba wstawić wewnątrz nawiasów tak, aby po wymnożeniu Twojego czynnika przez nawias otrzymać wyjściowy przykład.
Tak, czy inaczej warto w pamięci sprawdzić, czy po wymnożeniu otrzymanego czynnika przez utworzony nawias otrzymasz Twój przykład z podręcznika.
Jak wyłączyć wspólny czynnik przed nawias – zadania
Wyłącz wspólny czynnik przed nawias na 3 sposoby.
\[8x – 16y + 4 = 4 \cdot \left( {\quad \quad \quad \quad \quad \quad } \right)\] \[8x – 16y + 4 = 2 \cdot \left( {\quad \quad \quad \quad \quad \quad } \right)\] \[8x – 16y + 4 = 16 \cdot \left( {\quad \quad \quad \quad \quad \quad } \right)\] \[50xy – 10x + 30{x^2}{y^2} = 10x \cdot \left( {\quad \quad \quad \quad \quad \quad } \right)\] \[50xy – 10x + 30{x^2}{y^2} = 10 \cdot \left( {\quad \quad \quad \quad \quad \quad } \right)\] \[50xy – 10x + 30{x^2}{y^2} = 2 \cdot \left( {\quad \quad \quad \quad \quad \quad } \right)\]W zależności od przykładu można wyłączyć czynnik na wiele sposobów. Najczęściej stosuje się wyłączenie maksymalne tzn. wyłączasz największy czynnik jaki możesz. W niektórych przypadkach warto wyłączyć inny czynnik, ale decyzję trzeba uzależnić od kontekstu zadania.
Uzasadnij, że dla n naturalnego każda liczba postaci 2n+2n+1+2n+2+2n+3 jest podzielna przez 5.
Uwaga: Zadanie z potęgowania wykorzystuje w swoim rozwiazaniu wyłączanie najmniejszej potęgi przed nawias.- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Dana jest liczba rzeczywista a. Wyznacz wszystkie liczby x spełniające równanie:
x2 – a2 + x – a = 0
Dana jest liczba rzeczywista a. Wyznacz wszystkie liczby x spełniające równanie:
x2 – a2 + x – a = 0
Uzasadnij, że następujące wyrażenia arytmetyczne: \(2000\frac{7}{13}\cdot 2001\frac{7}{13}-1999\frac{7}{13}\cdot 2002\frac{7}{13}\) i \(6000\cdot 6001-5999\cdot 6002\) mają tę samą wartość.
Treść dostępna po opłaceniu abonamentu.Wykaż, że liczba 20162016+2·20162015+20162014 jest podzielna przez 2017.
Uwaga: Zadanie polega na umiejętnym wyłączeniu wspólnego czynnika przed nawias. Treść dostępna po opłaceniu abonamentu.- Zapisywanie wyrażeń algebraicznych
- Porządkowanie jednomianów
- Oblicz wartość liczbową wyrażenia
- Redukcja wyrazów podobnych
- Wyłączanie wspólnego czynnika przed nawias
- Mnożenie sum algebraicznych
- Wzory skróconego mnożenia
- Wyrażenia algebriaczne – sprawdzian
- Kurs: Wyrażenia algebraiczne z egzaminów gimnazjalnych