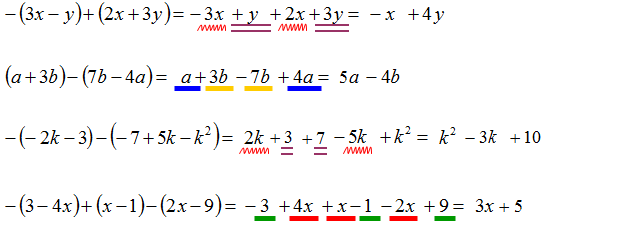Redukcja wyrazów podobnych
Usuwanie nawiasów jest dość proste. Jeśli przed nawiasem jest znak „-„, wówczas zmieniasz znaki wewnątrz nawiasów na przeciwne. Jeśli przed nawiasem jest znak „+”, wówczas opuszczasz nawiasy bez zmiany znaków.
Po usunięciu nawiasów zazwyczaj należy wykonać redukcję wyrazów podobnych. Najlepiej to zrobić przez podkreślenie wyrazów podobnych w ten sam sposób. Taka metoda jest pomocna i chroni przed pomyłkowym pominięciem określonego wyrażenia algebraicznego.
Wyrazy podobne – mówiąc w skrócie to takie, które mają takie same literki podniesione do tej samej potęgi. Jeśli występują w jednomianach pierwiastki to też muszą być z tej samej liczby i tego samego stopnia.
Jednomiany podobne mogą różnić się znakiem i liczbą stojącą przed symbolami.
Zredukuj wyrazy podobne – zadania
Usuń nawiasy i zredukuj wyrazy podobne.
\[2x + \left[ {3 – \left( {x – 1} \right)} \right] = \] \[\left( {5 – 2x} \right) – \left[ {\left( {3 – x} \right) – \left( {x + 2} \right)} \right] = \] \[ – 5a – \left[ {3b – \left( {{b^2} + 1} \right)} \right] + \left[ {\left( { – {b^2} + b} \right) – 1} \right] = \]W wyrażeniach algebraicznych, w których występuje kilka nawiasów zagnieżdżonych jeden w drugim należy wykonywać działania najpierw w nawiasie wewnętrznym i doprowadzić do jego usunięcia. Na końcu należy usuwać nawiasy zewnętrzne. Najczęściej są to nawiasy kwadratowe „[]” lub klamrowe „{}”.
Wykonaj mnożenie lub dzielenie jednomianów.
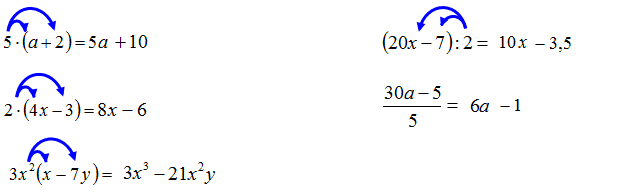
Wykonując mnożenie jednomianu przez sumy algebraiczne, należy wykonać działanie z każdym elementem sumy występującym w nawiasie. Na początku nauki warto rysować strzałki w celu podkreślenia tego faktu.
Wykonaj mnożenie lub dzielenie. Zredukuj wyrazy podobne.
\[\frac{{5x – 4}}{2} – 2\left( {x – 1} \right) = \] \[\frac{{12x – 42}}{6} – \frac{{9x + 15}}{3} = \] \[-\frac{-36+3x}{18}+\frac{-2x+16}{4}=\] \[3{{x}^{2}}-\frac{21{{x}^{2}}-49}{14}\cdot 2-5\cdot \frac{27x+30}{15}=\]- Zapisywanie wyrażeń algebraicznych
- Porządkowanie jednomianów
- Oblicz wartość liczbową wyrażenia
- Redukcja wyrazów podobnych
- Wyłączanie wspólnego czynnika przed nawias
- Mnożenie sum algebraicznych
- Wzory skróconego mnożenia
- Wyrażenia algebriaczne – sprawdzian
- Kurs: Wyrażenia algebraiczne z egzaminów gimnazjalnych