Twierdzenie Pitagorasa – Dowód
Dowód Twierdzenia Pitagorasa można przedstawić w postaci tzw. układanki. Spójrz na rysunek niżej.
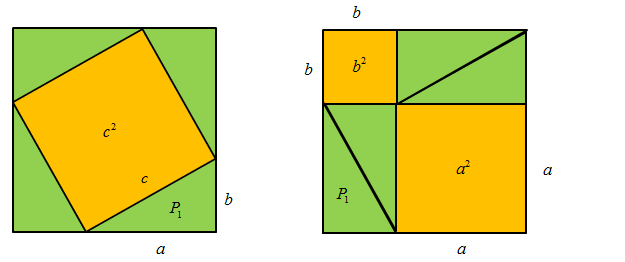
Wewnątrz dużego kwadratu budujesz 4 odcinki o takiej samej długości „c”, które tworzą żółty kwadrat o boku właśnie „c”. Każdy zaś bok dużego kwadratu ma długość „a + b”. Na pewno zauważyłeś, że każdy z zielonych trójkątów z obu rysunków ma boki o długości: a, b, c.
Dalej najważniejsze jest, abyś zauważył, że pole żółtego kwadratu o boku „c” z lewej strony jest równe sumie pól kwadratów żółtych o bokach „a” i „b” z prawej strony, czyli wzór c2 = a2 + b2.
Dlaczego?
Ta równość jest prawdziwa, ponieważ w identycznym największym kwadracie w lewej jak i z prawej strony występują takie same cztery zielone trójkąty. Zatem jeśli od największego kwadratu odejmę zarówno z lewej jak i z prawej strony takie same cztery zielone trójkąty wówczas pozostałe żółte pola z obu rysunków będą równe, czyli c2 = a2 + b2.
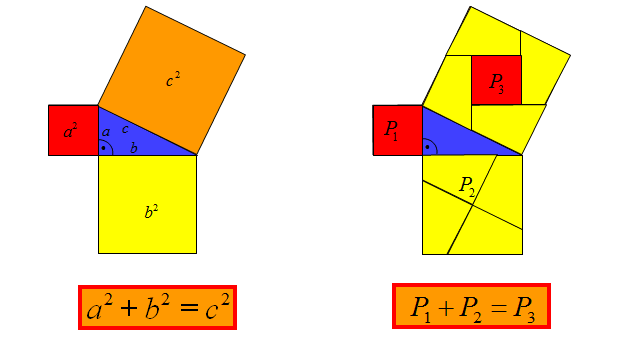
Najważniejsze jest tutaj, aby zauważyć, że dwa mniejsze kwadraty zbudowane na przyprostokątnych mają pola równe kwadratowi zbudowanemu na przeciwprostokątnej. Sposób na przełożenie kwadratów wyciętych z papieru, zbudowanych na trójkącie prostokątnym jest dość dużo. Przedstawiam Ci jeden z takich sposobów.