Liczby trójkątne i wielokątne
Jak zdefiniować liczby trójkątne? Najlepiej opisać je na podstawie rysunku:
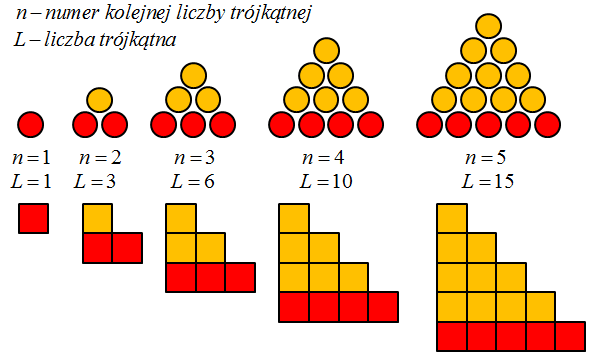
- Pierwszą liczbą trójkątną jest 1 – na rysunku to jedna kulka.
- Druga liczba trójkątna to 3 – na ilustracji do 1 kulki dorysowujemy warstwę 2 kulek poniżej pierwszej kulki. Łącznie 3 kulki.
- Trzecia liczba trójkątna to 6 – na prezentacji do istniejących już 6 kulek dodajemy warstwę, w której jest o 1 kulkę więcej niż w dotychczasowej najliczniejszej warstwie.
- Takie rozumowanie kontynuujemy w nieskończoność.
Przykłady 20 pierwszych liczb trójkątnych
| Numer liczby trójkątnej | Liczba trójkątna |
| 1 | 1 |
| 2 | 3 |
| 3 | 6 |
| 4 | 10 |
| 5 | 15 |
| 6 | 21 |
| 7 | 28 |
| 8 | 36 |
| 9 | 45 |
| 10 | 55 |
| 11 | 66 |
| 12 | 78 |
| 13 | 91 |
| 14 | 105 |
| 15 | 120 |
| 16 | 136 |
| 17 | 153 |
| 18 | 171 |
| 19 | 190 |
| 20 | 210 |
Kolejna n-ta liczba trójkątna składa się z sumy n kolejnych liczb naturalnych: \(T_{n} =1+2+3+4+…+n\)
Wzór na n-tą liczbę trójkątną
Wzór na n-tą liczbę trójkątną ma postać: \(T _{n} = \frac{n\cdot\big(n+1\big)}{2}\)
Można również rozpisać wzór na n-tą liczbę trójkątną przy pomocy symbolu Newtona. Każda kolejna liczba trójkątna jest równa odpowiedniemu współczynnikowi newtonowskiemu: \(T_{n} =\binom{n+1}{2}\)
Niżej przedstawiam zadanie z konkursu kuratoryjnego dla gimnazjum, w którym wyprowadzam wzór na n-tą liczbę trójkątną oraz korzystam z uzyskanego zapisu do wyznaczenia wybranej liczby trójkątnej.
Każdą liczbę trójkątną można przedstawić w postaci sumy kolejnych, początkowych liczb naturalnych: Tn=1+2+…+n
- Dziesiąta liczba trójkątna jest wielokrotnością liczby 11. PRAWDA/FAŁSZ
- Suma siódmej i ósmej liczby trójkątnej jest podzielna przez 16. PRAWDA/FAŁSZ
- Każdą liczbę trójkątną można zapisać w postaci \(T_{n}=\frac{n\big(n+1\big)}{2}\). PRAWDA/FAŁSZ
Rozwiązanie:
III.
Zaczniemy od końca tak będzie łatwiej.
Wyprowadzenie algebraiczne wzoru na n-tą liczbę trójkątną:
W tym wyprowadzeniu należy dodać do siebie dwa ciągi sum n liczb naturalnych. Jeden ciąg zaczynamy rozpisywać od najmniejszej liczby, drugi od końca, od największej liczby. Dalej należy otrzymane ciągi dodać pisemnie, tak jak poniżej na rysunku. W efekcie otrzymasz wzór na 2Tn, który składa się z n wyrażeń (n+1). Dalej otrzymane równanie 2Tn=n(n+1) dzielisz stronami przez 2 i otrzymasz szukany wzór na n-tą liczbę trójkątną Tn.

Graficzne wyprowadzenie wzoru na n-tą liczbę trójkątną:
Rozumowanie polega na zbudowaniu n-tej liczby trójkątnej z malutkich kwadracików jak na rysunku niżej i obliczeniu pola powstałej figury. Zauważ, maleńki kwadracik jest kwadratem jednostkowym, czyli ma bok o długości 1 i pole jego jest również równe 1. Kwadraciki tworzą strukturę podobną do schodków, w której jest n stopni. Chcąc obliczyć pole powstałej figury należy dorysować dwie linie, aby otrzymać kwadrat o boku n, a następnie dorysować przekątną. Pole pod przekątną jest trójkątem o podstawie n i wysokości n. Obliczamy to pole P=1/2n2.Teraz należy obliczyć n trójkącików wystających nad przekątną. Każdy z nich ma podstawę i wysokość równą 1. Zatem n takich trójkącików ma pole n⋅(1/2⋅1⋅1)=1/2n. Po dodaniu wszystkich pól otrzymujemy wzór na n-tą liczbę trójkątną.
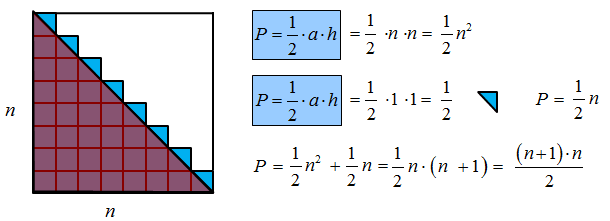
II.
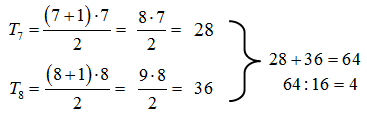
III.
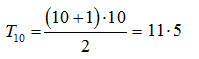
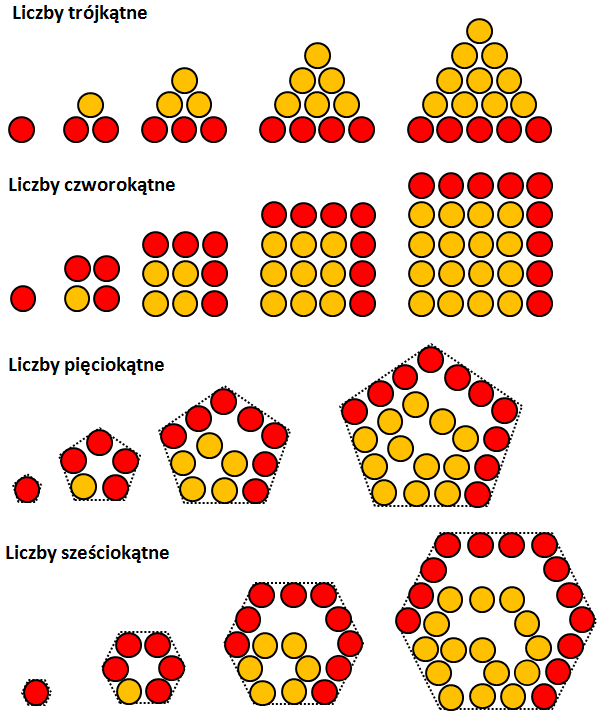
Liczby wielokątne: trójkątne, czworokątne …
Liczby wielokątne przedstawione graficznie tworzymy przez dokładanie kolejnych warstw zbudowanych z kulek tak, aby za każdym razem nasza figura była coraz to większa i zachowywała dany kształt.