Schemat Hornera

Schemat Hornera, inaczej metoda Hornera jest sposobem na dzielenie wielomianów.

Ograniczenia schematu Hornera

• Ważne: wykorzystując schemat Hornera do dzielenia wielomianów musisz mieć wielomian uporządkowany od najwyższej potęgi x.
• Dwumian, przez który dzielimy musi być stopnia pierwszego typu: (x+c) lub (x-c), gdzie c jest dowolną liczbą rzeczywistą.
• Metoda Hornera jest nieprzydatna, gdy dzielimy dany wielomian W(x) przez dwumian stopnia wyższego, niż pierwszy np. następujące dzielenie wielomianów:
  (2x³-4x²+x-3) : (x²-1)
  jest niewykonalne przez schemat Hornera. Zauważyłeś zapewne, że dwumian (x²-1) przez który dzielimy jest stopnia drugiego, a nie pierwszego. Takie działanie można wykonać przy pomocy metody pisemnej dzielenia wielomianów.

Metoda Hornera – Tabelka krok po kroku

W celu omówienia jak działa schemat Hornera podzielmy wielomian przez dwumian: \(\left( 2{{x}^{3}}-5{{x}^{2}}+4x-1 \right):\left( x-1 \right)\)

Krok 1: Budujesz tabelkę według podanego niżej schematu.

W pierwszym wierszu wpisujesz wszystkie kolejne współczynniki uporządkowanego wielomianu. Środkowy wiersz zostawiamy na obliczenia. W lewym dolnym rogu w trzecim wierszu tabelki wpisujesz liczbę, która jest miejscem zerowym dwumianu. W naszym przypadku to liczba 1 zeruje dwumian (x-1).

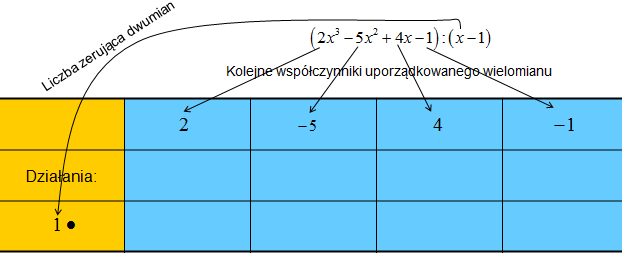
Uwaga: Wypisując wszystkie kolejne współczynniki wielomianu pamiętaj, że musisz wpisać do tabelki liczbę zero jeśli nie ma kolejnej potęgi wielomianu – ta potęga istnieje tylko, że ze współczynnikiem 0.

Przykład: Zapiszemy teraz wielomian W(x) z uwzględnieniem zerowych, niewidocznych współczynników.
W(x) = 7x⁴-2x³+1
W(x) = 7x⁴ -2x³ +0x² +0x¹ +1x⁰
Liczby w pierwszym wierszu tabeli: +7, -2, 0, 0, +1 są współczynnikami kolejnych potęg niewiadomej x.

Wielomian:
W(x) = 9x⁵-2x zapisujemy
W(x) = 9x⁵ +0x⁴ +0x³ +0x² -2x¹ +0x⁰
Wykonując dzielenie wielomianu W(x) schematem Hornera w pierwszym wierszu tabelki wystąpią odpowiednio liczby: +9, 0, 0, 0, -2, 0.

Krok 2: Przepisujesz pierwszy współczynnik bez zmian do dolnego wiersza

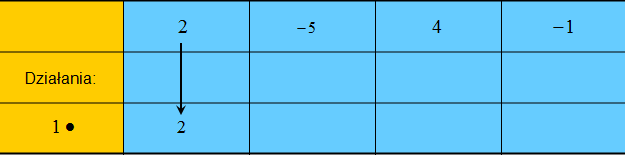
Krok 3: Tak otrzymaną liczbę 2 mnożysz przez liczbę 1, która jest miejscem zerowym dwumianu, następnie odejmujesz liczbę 5, współczynnik z pierwszego wiersza. Wynik będący liczbą (-3) wpisujesz do kolejnej komórki dolnego wiersza w schemacie Hornera.

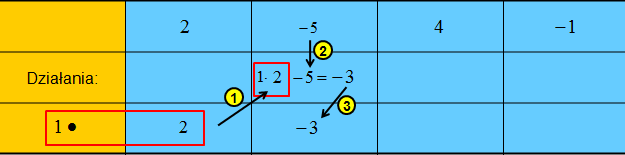
Krok 4: Wykonujemy podobne obliczenia jak w kroku 3.
Otrzymaną liczbę (-3) mnożysz przez 1, czyli przez miejsce zerowe dwumianu. Otrzymujesz (-3). Dalej dodajesz liczbę 4, która jest kolejnym współczynnikiem wielomianu. Wynik, liczbę 1 wpisujesz do dolnego wiersza.

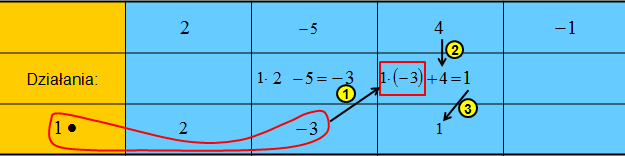
Krok 5: Dalej otrzymaną liczbę 1 mnożysz przez 1, czyli miejsce zerowe dwumianu. Otrzymujesz wynik 1. Od tej liczby odejmujesz ostatni współczynnik z pierwszego wiersza. Wynik 0 zapisujesz w prawej dolnej komórce tabeli.

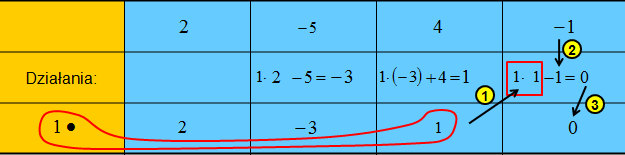
Niżej podaję całą uzupełnioną tabelkę ilustrującą schemat Hornera:

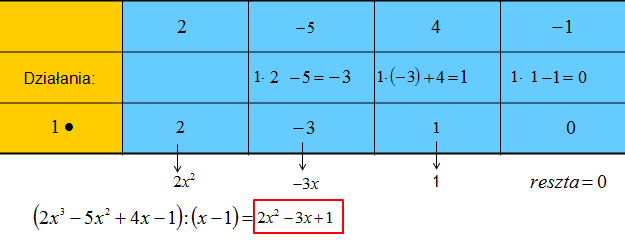
Rozwiązanie zadania wideo