Dzielenie wielomianów
Dzielenie wielomianów wykonujemy dwoma sposobami:
- Dzielenie wielomianów przez schemat Hornera.
- Dzielenie wielomianów metodą pisemną.
Dzielenie pisemne wielomianów
Zadanie.
Wykonaj dzielenie wielomianu przez dwumian: \[\left( 2{{x}^{3}}-5{{x}^{2}}+4x-1 \right):\left( x-1 \right)\]
Dzielenie wielomianów podobne jest do dzielenia liczb całkowitych, gdzie podczas dzielenia otrzymujemy iloraz (wynik dzielenia) i resztę z dzielenia.
Uwaga: Dzielenie wielomianów należy zacząć od uporządkowania wielomianów od największej do najmniejszej potęgi zmiennej x.
Przykład dzielenia pisemnego wielomianów:
\[\left( 2{{x}^{3}}-5{{x}^{2}}+4x-1 \right):\left( x-1 \right)\] Wielomian \(W(x)=\left( 2{{x}^{3}}-5{{x}^{2}}+4x-1 \right)\) będę nazywał dzielną, a dwumian \(Q(x)=\left( x-1 \right)\) dzielnikiem.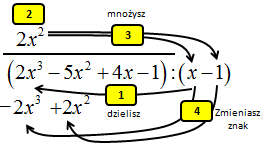
1. Dzielisz pierwszy jednomian 2x3 przez x.
2. Wynik dzielania: 2x2 wpisujesz nad poziomą kreską.
3. Jednomian: 2x2 znad kreski mnożysz przez dwumian (x-1)
4. Wykonując mnożenie z pkt.3 zmieniasz znaki w wyniku na przeciwne i taką postać wpisujesz pod wielomianem W(x). Podpisuj dokładnie jednomiany pod jednomianami tego samego stopnia zmiennej x.
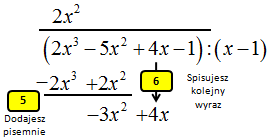
5. Podkreślasz działanie i dodajesz pisemnie, redukując jednomiany tego samego stopnia.
6. Spisujesz jednomian 4x z wielomianu W(x).
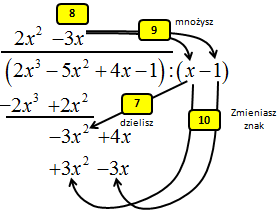
7. Dzielisz najwyższą potęgę w wielomianie -3x2+4x przez x pochodzący z dwumianu (x-1)
8. Wynik dzielenia (-3x) zapisujesz nad górną kreską.
9. Jednomian (-3x) mnożysz przez dwumian (x-1).
10. Wykonując mnożenie z pkt.9 zmieniasz znaki na przeciwne i tak otrzymany wynik podpisujesz pod najniższym istniejącym w zapisie wielomianem. Pamiętaj o podpisywaniu jednomianów pod jednomianami tego samego stopnia zmiennej x.
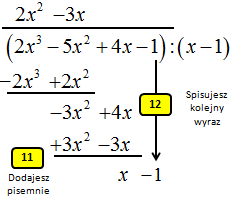
11. Podkreślasz dwa najniżej zapisane wielomiany, wykonując ich redukcję.
12. Spisujesz kolejny jednomian z górnego wielomianu W(x).
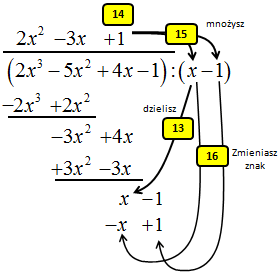
13. Najwyższą potęgę wielomianu: (x-1) dzielisz przez x.
14. Wynik 1 wpisujesz nad górną kreską.
15. Otrzymaną liczbę 1 mnożysz przez dwumian (x-1)
16. W wyniku mnożenia z pkt.15 zmieniasz wszystkie znaki na przeciwne. Zapisujesz ten wynik dbając o podpisywanie pod jednomianami tego samego stopnia.
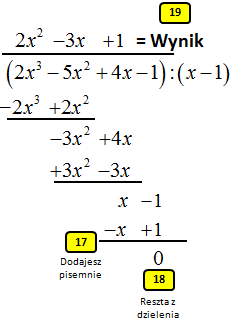
17. Podkreślasz i dodajesz pisemnie dwumiany.
18. Otrzymujesz liczbę 0, która jest resztą z dzielenia wielomianu. Potocznie mówimy wówczas, że otrzymaliśmy dzielenie wielomianów bez reszty.
19. Wielomian: 2x2-3x+1 powstały nad górną kreską jest ilorazem, czyli wynikiem dzielenia wielomianów.
Zadanie.
Wykonaj dzielenie wielomianu przez dwumian: \(\left( 2{{x}^{5}}+4{{x}^{4}}-{{x}^{3}}-2{{x}^{2}}+x+2 \right):\left( x+2 \right)\)
Zadanie.
Dzielenie wielomianów – 3 poziomy trudności w 10 przykładach. Zobacz film:
Zadanie.(poziom 1 łatwy)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik: \(\left( {{x}^{2}}-x-2 \right):\left( x+1 \right)\)
Zadanie.(poziom 1 łatwy)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik: \(\left( {{x}^{2}}+2x-63 \right):\left( x-7 \right)\)
Zadanie.(poziom 1 łatwy)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik. Podaj resztę z dzielenia wielomianu przez dwumian. \(\left( 2{{x}^{2}}+x+2 \right):\left( x-1 \right)\)
Zadanie.(poziom 1 łatwy)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik. Podaj resztę z dzielenia wielomianu przez dwumian. \(\left( 7{{x}^{3}}-34{{x}^{2}}+25x-3 \right):\left( x-4 \right)\)
Zadanie.(poziom 2 średni)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik. Podaj resztę z dzielenia wielomianu przez dwumian. \(\left( 2{{x}^{3}}-6{{x}^{2}}+x-3 \right):\left( x-3 \right)\)
Zadanie.(poziom 2 średni)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik. Podaj resztę z dzielenia wielomianu przez dwumian.
\[\left( 3{{x}^{5}}-6{{x}^{4}}+7{{x}^{3}}-14{{x}^{2}}-2x+4 \right):\left( x-2 \right)\]
Zadanie.(poziom 2 średni)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik. Podaj resztę z dzielenia wielomianu przez dwumian.
\[\left( 4{{x}^{4}}-3{{x}^{2}} \right):\left( x-1 \right)\]
Zadanie.(poziom 2 średni)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik. Podaj resztę z dzielenia wielomianu przez dwumian.
\[\left( 3{{x}^{6}}-2{{x}^{4}}+2{{x}^{2}}+1 \right):\left( x-1 \right)\]
Zadanie.(poziom 3 trudny)
Wykonaj dzielenie wielomianu przez dwumian i sprawdź otrzymany wynik. Podaj resztę z dzielenia wielomianu przez dwumian.
\[\left( 8{{x}^{3}}-4{{x}^{2}}+8x-9 \right):\left( {{x}^{2}}-3 \right)\]

Zadanie.(poziom 3 trudny)
Wykonaj dzielenie wielomianu przez wielomian i sprawdź otrzymany wynik. Podaj resztę z dzielenia tych wielomianów.
\[\left( 4{{x}^{4}}-2{{x}^{2}}+8x-1 \right):\left( 2{{x}^{2}}+x-1 \right)\]




