Twierdzenie Talesa – Sprawdzian
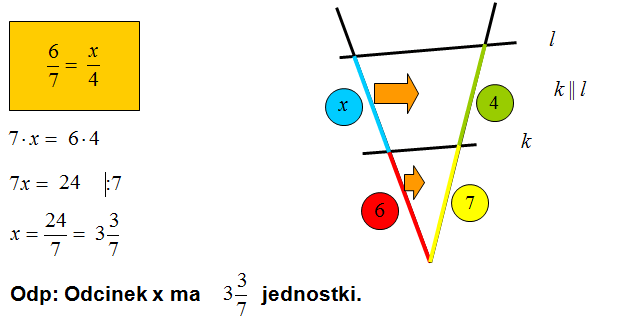
Na podstawie Twierdzenia Talesa oblicz długość odcinka oznaczonego literą x.
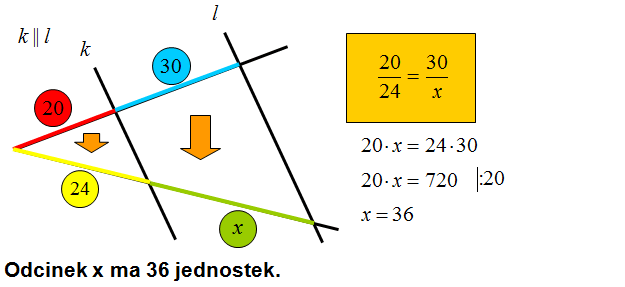
Powyższe zadanie można wytłumaczyć na wiele sposobów:
- Metoda spadających odcinków – Twierdzenie Talesa informuje nas, że proporcje możemy budować opuszczając odcinki z jednego ramienia kąta na odcinki z drugiego ramienia kąta. Strzałki pokazują kierunek spadania odcinków w Twierdzeniu Talesa.
- Metoda krokodylka – pokazuje jak można wpisać głowę krokodylka w dany kąt. Podczas zamknięcia paszczy tego krokodylka wybrane odcinki z górnej szczęki krokodylka łączą się odpowiadającymi odcinkami z dolnej szczęki. Nalaży tu zaznaczyć, że nie ma znaczenia, które ramię kąta będzie stanowiło górną szczękę krokodylka. Zawsze otrzymamy poprawne równanie.
Oczywiście jak zapewne wiesz z Twierdzenia Talesa można wyprowadzić kilka proporcji prowadzących do rozwiązania. Uważam, że proporcja przedstawiona powyżej jest najprostsza.
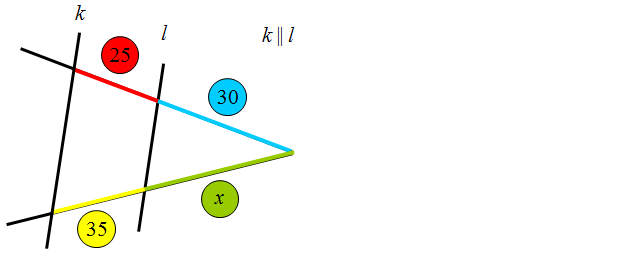
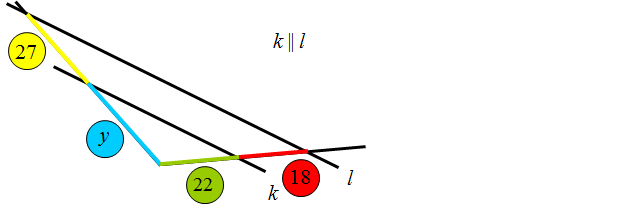
Na podstawie Twierdzenia Talesa oblicz literkę x.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
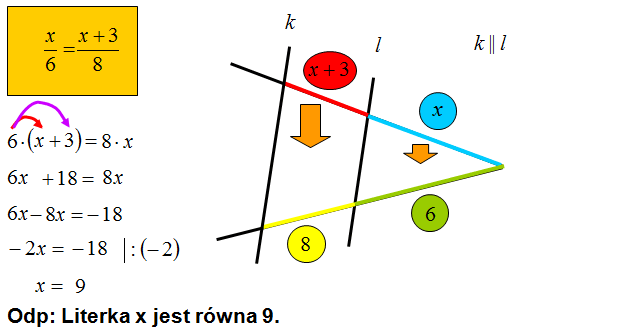
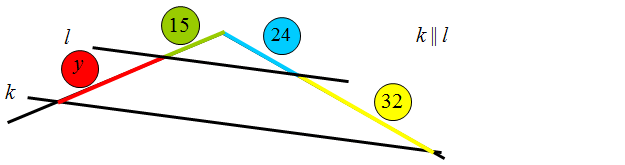
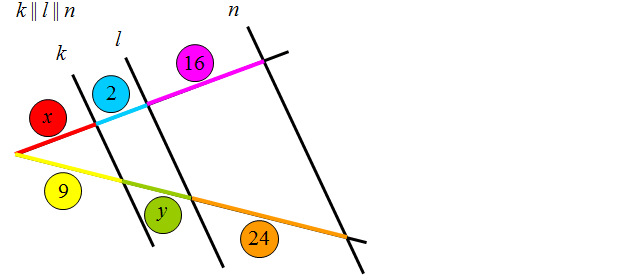
Oblicz długość odcinków oznaczonych literami x i y.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Tutaj mamy pozornie trudniejsze zadanie. Jak zastosujesz tutaj „spadanie odcinków” zadanie jest proste.
Odcinek czerwony spada na żółty, a różowy na pomarańczowy – zatem przechodząc na liczby otrzymujemy proporcję: \(\frac{x}{9}=\frac{16}{24}\). Po rozwiązaniu tej proporcji można zbudować kolejną w celu obliczenia niewiadomej y.
Widzimy, że odcinek niebieski spada na zielony, a różowy na pomarańczowy. Analizując tak „spadające odcinki” otrzymujemy równanie: \(\frac{2}{y}=\frac{16}{24}\).
Potrafisz rozwiązać zadania związane z Twierdzeniem Talesa?
Jeżeli nadal masz problemy z tym zagadnieniem, obejrzyj jeszcze raz wszystkie filmy przedstawione w tym artykule, które są idealnym materiałem powtórzeniowym do sprawdzianu zarówno w gimnazjum, jak i liceum.