Konkurs kuratoryjny z matematyki 2009/10 – Śląskie – Etap szkolny
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP SZKOLNY – 24 listopada 2009 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 13 zadań.
- Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj dokładnie treść zadań, zwracając uwagę na to, czy polecenie nakazuje podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- W części I (zadania od 1 do 8) wpisz TAK lub NIE obok każdej z trzech odpowiedzi. Za każdy poprawny wpis otrzymasz 1 punkt – w sumie za każde z tych zadań możesz otrzymać maksymalnie 3 punkty.
- Margines po prawej stronie kartki jest przeznaczony na brudnopis.
- Na rozwiązanie wszystkich zadań masz 90 minut.
- Aby zakwalifikować się do etapu rejonowego musisz zdobyć co najmniej 36 punktów.
Plik z zadaniami z konkursu kuratoryjnego – etap szkolny
Pobierz zadania matematyczne z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap szkolny
Ojciec i syn mają razem 147 lat. Ojciec ma dwa razy tyle lat, ile syn miał wtedy, kiedy ojciec miał tyle lat, ile syn ma teraz. Prawdą jest, że:
Do zbudowania regału stolarz potrzebuje następujących materiałów: 4 długie deski, 6 krótkich desek i 14 śrub. Prawdą jest, że:
Jeśli n jest dowolną liczbą naturalną dodatnią, to liczba 5n+5n+1:
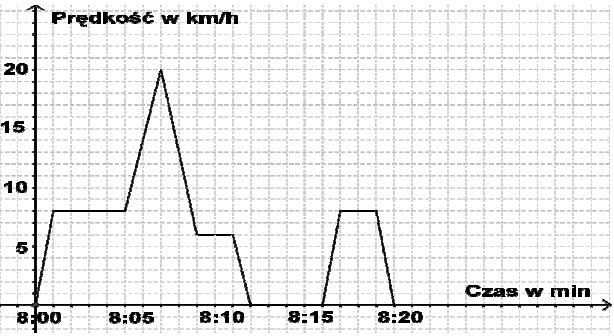
Poniższy wykres przedstawia prędkość rowerzysty podczas przejażdżki 20 minutowej. Na trasie był jeden podjazd (wtedy rowerzysta zwolnił, ale się nie zatrzymał) i jeden zjazd (wtedy rowerzysta przyśpieszył) oraz postój przed przejazdem kolejowym. Prawdą jest, że:
Liczby: 2x ; 2 ; x+3 są długościami boków trójkąta. Prawdą jest, że:
Sześciokąt foremny i trójkąt równoboczny mają równe obwody. Prawdą jest, że:
Dane są dwie proste równoległe. Jeśli na jednej z tych prostych zaznaczono 3 punkty, a na drugiej 2, to punkty te są wierzchołkami:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Bliźniaczymi liczbami pierwszymi nazywamy dwie liczby pierwsze różniące się od siebie o 2, np. 3 i 5. Prawdą jest, że:
II część konkursu kuratoryjnego z matematyki – zadania otwarte
W poniedziałek cena towaru wzrosła o 10%, w środę obniżono cenę tego towaru o 15%, a w piątek jeszcze raz obniżono o 20%. Oblicz jak i o ile procent zmieniła się cena towaru w ciągu tego tygodnia?
Treść dostępna po opłaceniu abonamentu.W ćwiartkę okręgu wpisano prostokąt tak, jak na rysunku. Oblicz pole zacieniowanego obszaru, jeżeli |OB|=|BC|=5.
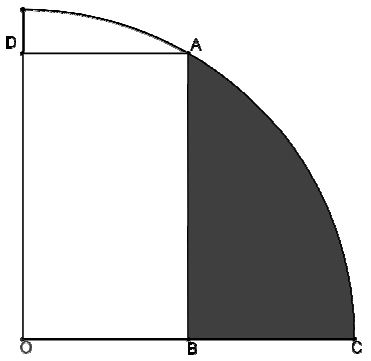Treść dostępna po opłaceniu abonamentu.
Sprawdź czy ułamki: \(\frac{37}{99}\,,\,\frac{3737}{9999}\quad i\quad \frac{373737}{999999}\) są równe.
Treść dostępna po opłaceniu abonamentu.Wykaż, że liczba \(\frac{1}{7+3\sqrt{3}}+\frac{1}{7-3\sqrt{3}}\) jest wymierna. (Uwaga: usuń niewymierość z mianownika).
Treść dostępna po opłaceniu abonamentu.Wyznacz najmniejszą liczbę naturalną taką, że 2/3 z niej jest liczbą trzycyfrową, a 3/4 z niej jest liczbą czterocyfrową. Odpowiedź uzasadnij.
Treść dostępna po opłaceniu abonamentu.