Konkurs kuratoryjny z matematyki 2002/03 – Śląskie – Etap szkolny
Konkurs przedmiotowy kuratoryjny z matematyki – etap szkolny 2002/2003.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z dwóch części. Pierwsza zawiera 10 zadań krótszych, druga 4 zadania rozszerzonej odpowiedzi. Przy numerze zdania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj uważnie treść zadań, zwracając uwagę na to, czy polecenie każe podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie lub w inny sposób uzasadnić wynik).
- Do następnego etapu zostają zakwalifikowani uczniowie, którzy uzyskają 25 punktów lub więcej.
- Czas na rozwiązanie wszystkich zadań wynosi 90 minut.
Pliki z pytaniami z konkursu kuratoryjnego
Zadania konkursowe do pobrania znajdziesz tutaj.
I część konkursu kuratoryjnego z matematyki.
Wyrażenie \(2\cdot {{4}^{11}}+3\cdot {{4}^{12}}+8\cdot {{4}^{10}}\) zapisz w postaci jednej potęgi.
Podaj cyfrę jedności liczby: 1 + 19991999
W zespole tanecznym liczba chłopców stanowi 80% procent liczby dziewcząt. Podaj, jaki procent liczby chłopców stanowi liczba dziewcząt?
Liczby x, y są dodatnie. Wskaż, które z wymienionych wyrażeń ma największą wartość:
Jedynym rozwiązaniem równania: A-(x-1)=1 jest liczba 1. Podaj, jaką liczbę należy wstawić w miejsce A.
Trzcina bambusowa o wysokości 32 łokci została złamana przez wiatr. Jej wierzchołek dotknął ziemi w odległości 16 łokci od podstawy. Oblicz, ile łokci nad ziemią została złamana trzcina.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
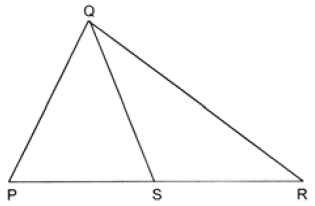
W trójkącie PQR |SP|=|SQ|=|SR| i |∠SQR|=42°.Oblicz, ile stopni ma kąt PQR?
Treść dostępna po opłaceniu abonamentu.
Marynarze mierzą kąty z pomocą jednostki kątowej zwanej rumbem. Rumb to kąt środowy oparty na łuku stanowiącym 1/32 część okręgu. Oblicz, ile rumbów ma kąt prosty?
Treść dostępna po opłaceniu abonamentu.Na każdej z dwóch prostych równoległych obrano po cztery różne punkty. Podaj maksymalną liczbę trójkątów, których wierzchołkami są te punkty.
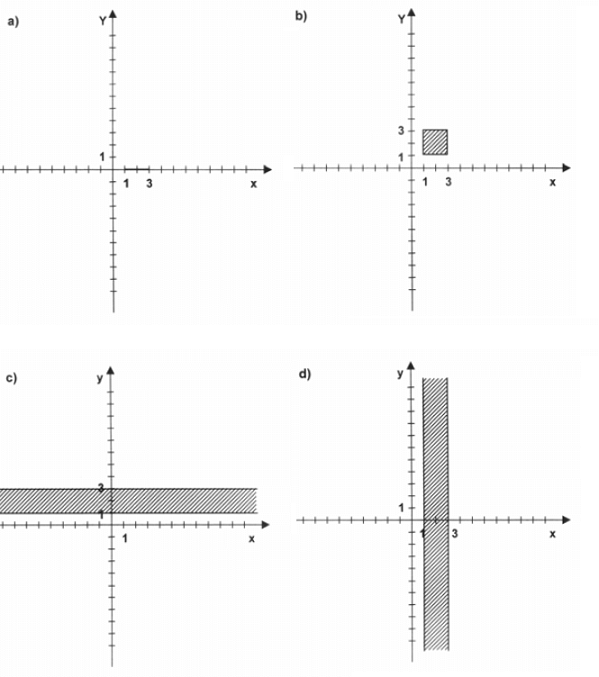
Treść dostępna po opłaceniu abonamentu.Wskaż, na którym z poniższych rysunków przedstawiony jest zbiór wszystkich punktów płaszczyzny, który współrzędne spełniają jednocześnie następujące warunki: 1≤x ≤3 i y∈R.
Treść dostępna po opłaceniu abonamentu.
II część konkursu kuratoryjnego z matematyki.
Wykresem pewnej funkcji jest prosta przechodząca przez punkt A = (− 2,3). Ponadto wiadomo, że dla argumentów mniejszych od 2 funkcja ta przyjmuje wartości dodatnie, zaś dla argumentów większych od 2 przyjmuje ona wartości ujemne. Znajdź wzór tej funkcji, obliczając potrzebne współczynniki.
Treść dostępna po opłaceniu abonamentu.Ojciec jest 5 razy, a dziadek 8 razy starszy od Janka. Suma lat przeżytych przez wszystkich trzech jest mniejsza od 112, ale większa od 84. Oblicz, ile lat ma każdy z nich.
Treść dostępna po opłaceniu abonamentu.Światła sygnalizacyjne na pewnym skrzyżowaniu zmieniają się w następującej kolejności: czerwone 90 sekund, czerwone i żółte 5 sekund, zielone 80 sekund, żółte 5 sekund, znowu czerwone itd. Oblicz, przez ile minut w ciągu doby pali się czerwone światło?
Treść dostępna po opłaceniu abonamentu.Wyznacz wszystkie liczby całkowite nieujemne n spełniające równanie: 2n⋅(4 − n) = 2n + 4
Treść dostępna po opłaceniu abonamentu.