Przykładowy egzamin ósmoklasisty z matematyki CKE 2019
Zobacz treści zadań i wideo odpowiedzi z przykładowego egzaminu ósmoklasisty z matematyki. Krok po kroku… Przekonaj się, że matematyka może być prosta. Bądź spokojny na egzaminie.
Egzamin ósmoklasisty matematyka, testy 8 klasisty, arkusze próbne, odpowiedzi ⇒Zobacz więcej⇐Testy z przykładowego egzaminu ósmoklasisty CKE
Czas pracy: 100 minut
Z okazji Światowego Dnia Książki uczniowie klasy VII zorganizowali quiz wiedzy o postaciach literackich. Quiz można było zakończyć na jednym z poziomów, które zaliczało się kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło quiz na danym poziomie. Na poziomach niższych niż Asia quiz zakończyło dokładnie 32% uczniów biorących w nim udział.
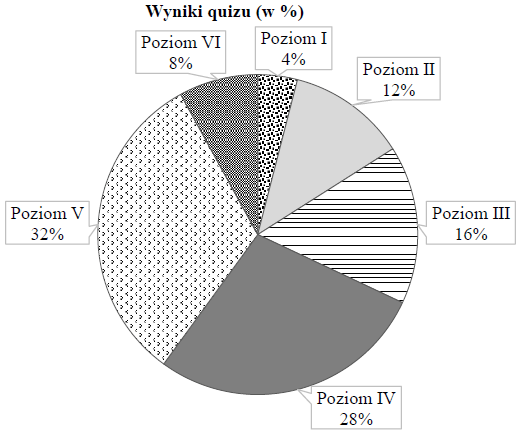
Ile procent uczniów zakończyło ten quiz na poziomach wyższych niż Asia? Wybierz właściwą odpowiedź spośród podanych.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 4,5 : 0,75 jest równa wartości wyrażenia A/B.
Wartość wyrażenia 1,25 ⋅ 0,4 jest równa wartości wyrażenia C/D.
Tata Bartka przed wyjazdem z Krakowa do Warszawy analizuje niektóre bezpośrednie połączenia między tymi miastami. Do wyboru ma cztery połączenia przedstawione w poniższej tabeli.
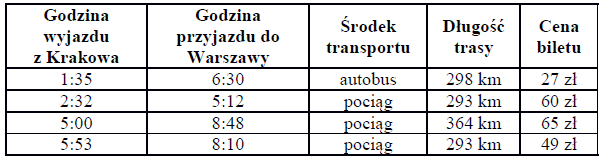
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Prosta EF dzieli prostokąt ABCD na kwadrat EFCD o obwodzie 32 cm i prostokąt ABFE o obwodzie o 6 cm mniejszym od obwodu kwadratu EFCD.
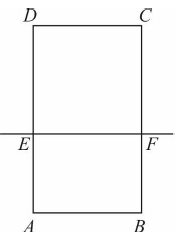
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość odcinka AE jest równa
Narysowany kwadrat należy wypełnić tak, aby iloczyny liczb w każdym wierszu, każdej kolumnie i na obu przekątnych kwadratu były takie same.
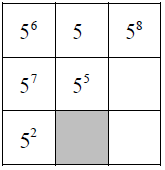
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Jacek i Ola testują swoje elektryczne deskorolki. W tym celu zmierzyli czasy przejazdu na trasie 400 m. Ola pokonała tę trasę w czasie 160 s, a Jacek – w czasie 100 s.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Różnica średnich prędkości uzyskanych przez Jacka i przez Olę jest równa
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:\[P=W+\frac{1}{2}B-1\]
gdzie P oznacza pole wielokąta, W – liczbę punktów kratowych leżących wewnątrz wielokąta, a B – liczbę punktów kratowych leżących na brzegu tego wielokąta.
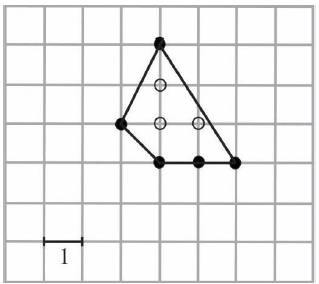
W wielokącie przedstawionym na rysunku W=3 oraz B=5, zatem P=4,5.
Wewnątrz pewnego wielokąta znajduje się 5 punktów kratowych, a na jego brzegu jest 6 punktów kratowych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego wielokąta jest równe
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wielokąt, którego pole jest równe 15, może mieć A/B punktów kratowych leżących na brzegu wielokąta.
Pole wielokąta, który ma dwukrotnie więcej punktów kratowych leżących na brzegu wielokąta niż punktów leżących wewnątrz, wyraża się liczbą C/D.
Z każdej z dwóch jednakowych kostek sześciennych wycięto sześcian i otrzymano bryły przedstawione na rysunku.
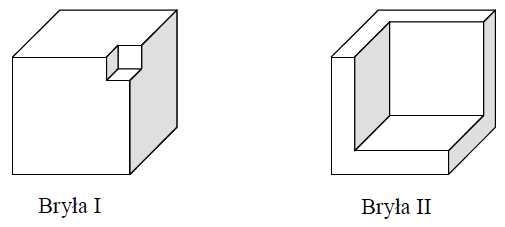
Czy całkowite pole powierzchni bryły I jest większe od całkowitego pola powierzchni bryły II? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Na bokach trójkąta prostokątnego ABC zaznaczono punkty D i E. Odcinek DE podzielił trójkąt ABC na dwa wielokąty: trójkąt prostokątny ADE i czworokąt DBCE, jak na rysunku. Odcinek AB ma długość \(4\sqrt{3}cm\), a odcinek DE ma długość 3cm.
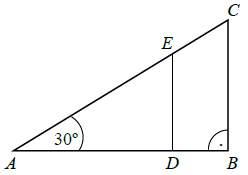
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość odcinka EC jest równa
Maja grała z przyjaciółmi w ekonomiczną grę strategiczną. W trakcie tej gry zainwestowała w zakup nieruchomości 56 tys. gambitów – wirtualnych monet. Po upływie 30 minut odsprzedała tę nieruchomość za 280 tys. gambitów.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość nieruchomości od momentu jej zakupienia do momentu sprzedaży
Przekątne prostokąta ABCD przedstawionego na rysunku przecinają się pod kątem 140°.
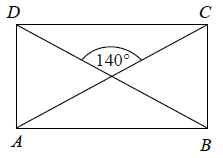
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba \(a=\sqrt{125}-1\) jest A/B.
Liczba \(a=4\sqrt{6}-10\) jest C/D.
Punkt S = (3, 2) jest środkiem odcinka AB, w którym A = (5, 5).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Punkt B ma współrzędne
Jedną ścianę drewnianego sześcianu pomalowano na czerwono, a pozostałe – na biało. Ten sześcian rozcięto na 27 jednakowych sześcianów.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest kwadratem o boku 5cm, a druga – prostokątem o bokach 3cm i 5cm.
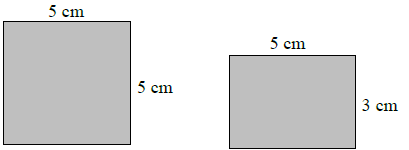
Oblicz sumę długości wszystkich krawędzi prostopadłościanu o takich wymiarach. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Ania i Jarek grali w kamienie. Na początku gry kamienie układa się w dwóch stosach. Następnie gracze wykonują ruchy na przemian. Ruch w grze polega na wzięciu dowolnej liczby kamieni tylko z jednego ze stosów. Przegrywa ten, kto nie może już wykonać ruchu. Na pewnym etapie gry pierwszy stos zmalał do jednego kamienia, a na drugim znajdowały się trzy kamienie. Ruch miała wykonać Ania. Uzasadnij, że aby zagwarantować sobie wygraną, Ania musiała wziąć dwa kamienie z drugiego stosu.
Treść dostępna po opłaceniu abonamentu.Na pływalni w marcu obowiązywała promocja.

Wojtek był w marcu codziennie jeden raz na pływalni i wykorzystał wszystkie ulgi promocyjne. Ile kosztowało go korzystanie z pływalni w marcu? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Trener chce zamówić 25 nowych piłek do tenisa. Piłki wybranej firmy sprzedawane są w opakowaniach po 3 sztuki albo po 4 sztuki. Ile opakowań każdego rodzaju powinien zamówić trener, aby mieć dokładnie 25 nowych piłek? Podaj wszystkie możliwości. Zapisz rozwiązanie.
Treść dostępna po opłaceniu abonamentu.Prostokątny pasek papieru o wymiarach 12 cm na 2 cm jest z jednej strony biały, a z drugiej – szary. Ten pasek złożono w sposób pokazany na rysunku.
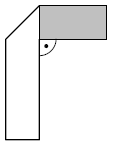
Pole widocznej szarej części paska jest równe 8cm2. Jakie pole ma widoczna biała część paska? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.W wypożyczalni Gierka za wypożyczenie gry planszowej trzeba zapłacić 8 zł za 3 dni i dodatkowo po 2,50 zł za każdy kolejny dzień wypożyczenia. Natomiast w wypożyczalni Planszówka płaci się 12 zł za 3 dni i po 2 zł za każdy kolejny dzień. Przy jakiej liczbie dni koszty wypożyczenia tej gry w jednej i drugiej wypożyczalni są jednakowe? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.



