Mediana
Co to jest mediana?
Mediana – to wartość środkowa w uporządkowanym ciągu liczb.
Przykład MEDIANYw uporządkowanym ciągu, w którym jest nieparzysta liczba elementów.
Dany ciąg uporządkowany rosnąco: 2, 5, 7, 8, 9, 10, 32. Zatem Mediana M=8, ponieważ jest to środkowy wyraz ciągu liczbowego. Jest to czwarty element niezależnie, czy liczysz od początku, czy od końca tego ciągu liczb.
Przykład MEDIANY w ciągu uporządkowanym rosnąco o parzystej liczbie elementów tego ciągu.
Dany ciąg uporządkowany rosnąco: 2, 3, 4, 5, 6, 7. Jeśli ciąg posiada parzystą ilość elementów, wówczas bierzemy sumę dwóch środkowych elementów i wyliczamy ich średnią arytmetyczną. W tym przypadku dwa wyrazy są środkowe, czyli równoodległe od początku i końca ciągu. Medianą będzie średnia arytmetyczna tych dwóch środkowych liczb: \(M=\frac{4+5}{2}=\frac{9}{2}=4,5\)
Jak obliczyć medianę?
Niżej przedstawiam zadania z mediany
W poniższej tabeli przedstawiono wynik sondażu przeprowadzonego w grupie uczniów dotyczącego czasu przeznaczonego dziennie na przygotowanie zadań domowych.
| Czas ( w godzinach) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Liczba uczniów | 5 | 10 | 15 | 10 |
W odniesieniu do liczba godzin, jaką uczeń przeznacza na przygotowanie zadań domowych, prawdą jest, że:
Dany jest zestaw dziesięciu liczb: 11, 14, 2, 3, 7, 6, 7, 8, 5, 2.
W pewnej firmie jest ośmiu pracowników. Ich zarobki w złotych to: 1700, 1800, 2000, 2000, 2100, 2100, 2100 i 8000. Prawdą jest, że:
W pewnej firmie średnia arytmetyczna miesięcznych zarobków wszystkich pracowników wynosi 2328 zł. Rozkład tych zarobków przedstawiono w tabeli.
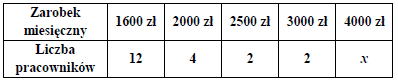
Ustal, która wartość jest większa: mediana czy średnia arytmetyczna miesięcznych zarobków pracowników tej firmy. Odpowiedź uzasadnij.
Mediana zadania z egzaminu gimnazjalnego
Na diagramie przedstawiono wyniki pracy klasowej z matematyki w pewnej klasie.
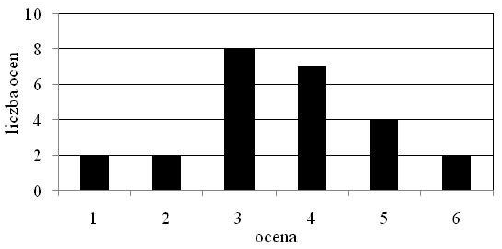
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że
(Uwaga: Mediany nie ma w podstawie programowej dla 8 klas w roku 2020.)
A. pracę klasową pisało 30 uczniów.
B. najczęściej powtarzającą się oceną jest 4.
C. mediana wyników z pracy klasowej wynosi 2.
D. średnia wyników z pracy klasowej jest równa 3,6.
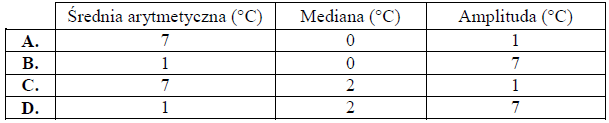
Ola codziennie, przez tydzień, odczytywała o 7 rano temperaturę powietrza. Oto podane (w °C) wyniki jej pomiarów: −2, 3, 4, 0, −3, 2, 3.
Wybierz odpowiedź, w której podano poprawne wartości średniej arytmetycznej, mediany i amplitudy (różnica między wartością najwyższą i wartością najniższą) zanotowanych temperatur.
(Uwaga: Mediana nie występuje w podstawie programowej szkoły podstawowej w roku 2020.)
Pięć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej: 1, a, b, c, 10. Mediana liczb: 1, a, b jest równa 3, a mediana liczb: a, b, c, 10 jest równa 5.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba c jest równa
Rozwiązanie:
Mediana to wartość środkowa w ciągu uporzadkowanym. Jeśli ciąg ma parzystą liczbę wyrazów to medianą jest średnia arytmetyczna dwóch środkowych wyrazów tego uporządkowanego ciągu.
Dany jest ciąg uporządkowany: 1, a, b, c, 10.
Wiemy, że medianą liczb: 1, a, b jest równa 3. Stąd możemy wywnioskować, że a=3.
Mamy ciąg uporządkowany: 1, a, b, c, 10. Wiedząc, że a=3 otrzymujemy ciąg liczb: 1, 3, b, c, 10.
Z zadania wiemy, że mediana liczb: 3, b, c, 10 jest równa 5.
Zatem b=4, c=6, ponieważ mediana liczb: 3, 4, 6, 10 jest równa 5, ponieważ średnia dwóch środkowychwyrazów 4 i 6 jest równa 5.
Inne możliwości są niedopuszczalne, ponieważ psują nam początkowe warunki zadania o rosnąco uporządkownych liczbach oraz o niepowtarzalności liczb w ciągu.
Odp.: C. 6
Do zestawu liczb: 3, 5 i 9 dopisano czwartą liczbę. Mediana otrzymanego w ten sposób zestawu czterech liczb jest większa od mediany początkowego zestawu trzech liczb. Uzasadnij, że dopisana liczba jest większa od 5.




