Konkurs kuratoryjny z matematyki 2016/17 – Śląskie – Etap wojewódzki
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP WOJEWÓDZKI
Przeczytaj uważnie poniższą instrukcję:
- Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod ustalony przez komisję.
- Sprawdź, czy arkusz konkursowy zawiera 8 stron (zadania 1-14).
- Czytaj uważnie wszystkie teksty i zadania.
- Rozwiązania zapisuj długopisem lub piórem. Nie używaj korektora.
- Staraj się nie popełniać błędów przy zaznaczaniu odpowiedzi, ale jeśli się pomylisz, błędne zaznaczenie otocz kółkiem ⊗ i zaznacz inną odpowiedź znakiem „x”.
- W zadaniach typu PRAWDA/FAŁSZ oceń, czy podane zdania są prawdziwe, czy fałszywe. Zaznacz właściwą odpowiedź.
- Rozwiązania zadań otwartych zapisz czytelnie w wyznaczonych miejscach. Pomyłki przekreślaj.
- Przeczytaj uważnie treść zadań, zwracając uwagę na to, czy polecenie każe podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie lub w inny sposób uzasadnić wynik).
- Przygotowując odpowiedzi na pytania, możesz skorzystać z miejsc opatrzonych napisem Brudnopis. Zapisy w brudnopisie nie będą sprawdzane i oceniane.
- Podczas rozwiązywania zadań nie wolno Ci korzystać z kalkulatora.
- Czas pracy: 120 minut.
Plik z zadaniami z konkursu kuratoryjnego – etap wojewódzki
Zadania z konkursu kuratoryjnego w pliku pdf.
Rozwiąż krzyżówkę, wpisując litery w odpowiednie pola. Hasło w zacieniowanych okienkach, to pojęcie oznaczające odległość liczby rzeczywistej od zera. Hasło nie jest oceniane.
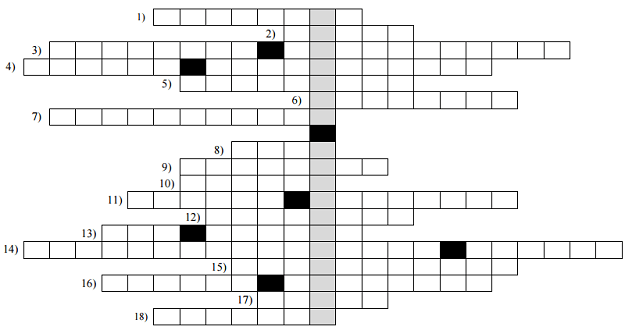1) W walcu i stożku jest kołem.2) Bryła obrotowa, której powierzchnia boczna po rozwinięciu jest prostokątem.
3) Trójkąty podobne w skali 1:1.
4) Proste zawierające przyprostokątne w trójkącie prostokątnym.
5) Figura będąca jednym z ramion kąta.
6) Wielkość oznaczona literą d we wzorze na długość okręgu: L=πd.
7) Własność liczby gwarantująca dzielenie się tej liczby bez reszty przez inną liczbę.
8) Równoległobok, którego przekątne są wzajemnie prostopadłe.
9) Jednostka długości 10000 razy mniejsza od kilometra.
10) Czworokąt posiadający co najmniej jedną parę boków równoległych.
11) Liczba, która ma rozwinięcie dziesiętne skończone albo nieskończone okresowe.
12) Odcinek łączący wierzchołek stożka z punktem na okręgu jego podstawy.
13) Część okręgu wyznaczona przez ramiona kąta środkowego.
14) Zależność między dwoma wielkościami zmiennymi, których iloraz pozostaje stały.
15) Działanie, które należy wykonać jako pierwsze w wyrażeniu: 1510-115.
16) Dwie liczby, których iloczyn jest równy 1.
17) Część wspólna koła i stycznej do tego koła.
18)Jednostka czasu równa 1/3600 godziny
W zadaniach od 2. do 10. oceń, czy podane zdania są prawdziwe, czy fałszywe. Zaznacz właściwą odpowiedź.
Funkcja f określona jest tylko dla liczb całkowitych nieujemnych i każdej z tych liczb przyporządkowuje liczbę mniejszą od niej o 5,5.
Liczby a, b, c spełniają warunki: abc=–100 i a+b=0
W trójkącie ABC wysokość CD o długości 12cm dzieli bok AB na odcinki AD i BD, takie że długość AD wynosi 8cm, a długość BD wynosi 16cm.
Dane są liczby: a=610 i b=125. Wtedy
Średnio 100 g chleba proteinowego zawiera tyle węglowodanów, co 10 g chleba żytniego razowego lub 8 gramów pieczywa pszennego.
Za 5kg cytryn i 6kg mandarynek zapłacimy tyle samo, co za 7,5kg cytryn i 4kg mandarynek. Jeżeli cytryny podrożeją o 25%, a cena mandarynek obniży się o 20%, to za 100zł kupimy 12kg cytryn i 10kg mandarynek.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Dane są bryły: walec o średnicy podstawy długości 12cm i wysokości 5cm oraz stożek o promieniu podstawy 3cm i wysokości 60cm.
Wybieramy losowo dwa wierzchołki ośmiokąta foremnego. Prawdopodobieństwo tego, że odcinek o końcach w wylosowanych punktach jest
Wykaż, że liczba 20162016+2·20162015+20162014 jest podzielna przez 2017.
Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
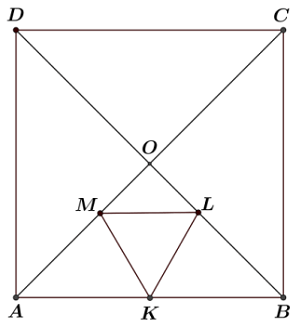
Dany jest kwadrat ABCD. Trójkąt równoboczny KLM, o boku długości 4cm, wpisano w trójkąt ABO w ten sposób, że odcinki AB i ML są równoległe. Oblicz pole kwadratu ABCD.
Treść dostępna po opłaceniu abonamentu.
Trójkąt prostokątny o przyprostokątnych długości 5cm i 12cm obraca się wokół prostej zawierającej przeciwprostokątną. Wykonaj rysunek pomocniczy. Oblicz pole powierzchni całkowitej otrzymanej bryły.
Treść dostępna po opłaceniu abonamentu.