Konkurs kuratoryjny z matematyki 2016/17 – Śląskie – Etap szkolny
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP SZKOLNY
Informacje dla ucznia:
- Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod ustalony przez komisję.
- Sprawdź, czy arkusz konkursowy zawiera 8 stron (zadania 1-13).
- Czytaj uważnie wszystkie teksty i zadania.
- Rozwiązania zapisuj długopisem lub piórem. Nie używaj korektora.
- Staraj się nie popełniać błędów przy zaznaczaniu odpowiedzi, ale jeśli się pomylisz, błędne zaznaczenie otocz kółkiem ⊗ i zaznacz inną odpowiedź znakiem „x”.
- W zadaniach typu PRAWDA/FAŁSZ oceń, czy podane zdania są prawdziwe, czy fałszywe. Zaznacz właściwą odpowiedź.
- Rozwiązania zadań otwartych zapisz czytelnie w wyznaczonych miejscach. Pomyłki przekreślaj.
- Przygotowując odpowiedzi na pytania, możesz skorzystać z miejsc opatrzonych napisem Brudnopis. Zapisy w brudnopisie nie będą sprawdzane i oceniane.
- Podczas rozwiązywania zadań nie wolno Ci korzystać z kalkulatora.
- Czas pracy: 120 minut
Plik z zadaniami z konkursu kuratoryjnego – etap szkolny
Zadania z konkursu kuratoryjnego w pliku pdf.
Rozwiąż krzyżówkę. Hasło w zacieniowanych okienkach, to znane Ci pojęcie matematyczne. Hasło nie jest oceniane, ale zweryfikuje Twoje odpowiedzi.

- W trapezie prostokątnym odcinek pokrywający się z jednym z ramion.
- Jeden z dziesięciu znaków pozwalających zapisać liczbę w systemie dziesiętnym.
- Wielkość opisująca kąt, wyrażana w stopniach.
- Jednostka pola powierzchni równa 0,01km2.
- Wynik jednego z działań arytmetycznych.
- Wyrażenie będące iloczynem liczby i zmiennej połączone znakiem mnożenia.
- Mianownik ułamka rozumianego jako zapis dzielenia.
- Najdłuższa cięciwa okręgu.
- x w równaniu: 3x+5(x+1)=8x .
- Czworokąt, który jest jednocześnie rombem i prostokątem.
- Zapisywany nad kreską ułamkową.
- Czworokąt posiadający dwie pary boków równoległych.
- Jedna z półprostych wyznaczających środek okręgu wpisanego w trójkąt.
- Dla sześcianu o krawędzi a jest równa a3.
- Równoległobok posiadający wszystkie boki równe.
- Liczba 100 w wyrażeniu 75100.
- Jeden z odcinków wyznaczających kąt środkowy.
- Może być, np. naturalna, całkowita, wymierna.
- Zbiór argumentów funkcji.
- Pierwsze w kolejności działanie do wykonania w wyrażeniu: 3⋅105+84:32.
- Dla każdego trójkąta można poprowadzić jedną taką prostą, trzy albo taka prosta nie istnieje.
W zadaniach od 2. do 9. oceń, czy podane zdania są prawdziwe, czy fałszywe. Zaznacz właściwą odpowiedź.
Średnia arytmetyczna wzrostu chłopców w klasie 3a gimnazjum wynosi 170 cm, a dziewcząt 160 cm. Do klasy doszły dwie osoby, ale średnie wzrostu chłopców i dziewcząt nie zmieniły się.
Bluza jest o 5 zł droższa od koszuli. Gdyby cenę bluzy obniżono o 20%, a koszuli podniesiono o 4%, to wtedy cena bluzy stanowiłaby 80% ceny koszuli.
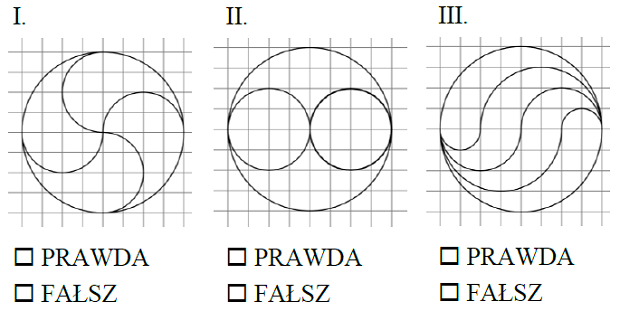
Podział koła na 4 części o równych polach przedstawia rysunek:
W trapezie trzy boki mają długość a , a czwarty bok ma długość 2a.
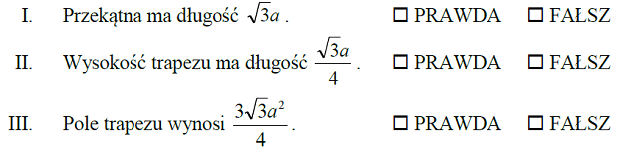
Dany jest zestaw dziesięciu liczb: 11, 14, 2, 3, 7, 6, 7, 8, 5, 2.
Dane jest wyrażenie 12:x-6⋅x , w którym x jest liczbą naturalną, różną od zera.
Oblicz pole trójkąta o wierzchołkach: A(2,1), B(–5,4), C(–1,–2).
Reszty z dzielenia liczb całkowitych a, b, c przez 5 wynoszą odpowiednio 1, 2, 3. Wyznacz resztę z dzielenia:
a) sumy kwadratów liczb a, b, c przez 5,
b) kwadratu sumy liczb a, c przez 5.
Akwarium ma kształt prostopadłościanu. Wewnątrz akwarium jego wysokość wynosi 3 dm, a podstawa ma wymiary 4dm × 5dm. Do akwarium wlano wodę do wysokości o 1 cm mniejszej niż wysokość akwarium. Sprawdź, wykonując odpowiednie obliczenia, czy bez wylania wody można całkowicie zanurzyć w tym akwarium kulkę o objętości 0,5π [dm3]
Ania i Wojtek wyruszyli na trening nordic walking jednocześnie z tego samego miejsca i w tym samym kierunku. Wojtek szedł 2,25h ze stałą prędkością 6km/h. Po odpoczynku, który trwał 25 minut wyruszył w drogę powrotną, utrzymując stałą prędkość 5,5km/h. Ania szła stale z prędkością 4,5km/h. Wyznacz czas, jaki upłynął od momentu startu do momentu spotkania Ani i Wojtka oraz odległość od miejsca wyjścia do miejsca spotkania.





