Konkurs kuratoryjny z matematyki 2016/17 – Śląskie – Etap rejonowy

Rozwiąż krzyżówkę, wpisując cyfry w odpowiednie pola. Hasło w zacieniowanych okienkach, to część rozwinięcia wyniku dzielenia liczb 2016 i 2017. Hasło nie jest oceniane.

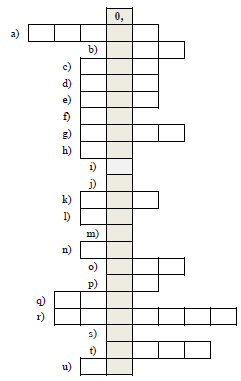
1. Największa liczba pięciocyfrowa.
2. Największa trzycyfrowa liczba będąca kwadratem liczby naturalnej.
3. Liczba, której odległość na osi liczbowej od 752 i od 838 jest taka sama.
4. Średnia arytmetyczna kolejnych liczb naturalnych od 101 do 199.
5. Wartość bezwzględna największej liczby całkowitej mniejszej od (–108).
6. Wynik działania: 30-8⋅5+24.
7. Długość przekątnej kwadratu o boku \(300\sqrt{8}\).
8. Największa dwucyfrowa potęga liczby 3.
9. Wartość wykładnika x w wyrażeniu 27^x=3¹².
10. Iloczyn liczb wzajemnie odwrotnych.
11. Liczba, której zapis w systemie rzymskim ma postać: DCCLXXVII.
12. Mediana zbioru liczb: 20, 19, 15, 15, 23, 23, 15.
13. Wartość wyrażenia \(\frac{\sqrt{56}}{\sqrt{14}}:\frac{1}{2}\).
14. Największa dwucyfrowa liczba pierwsza.
15. Powierzchnia 40000m² wyrażona w arach.
16. Promień kuli o polu powierzchni P=6400π.
17. Mianownik w wyniku działania \({{\left( \frac{2}{5} \right)}^{-8}}\).
18. Przybliżenie liczby 1 170 999 z dokładnością do rzędu tysięcy.
19. Suma rozwiązań równania: |x|-8= 0 .
20. Liczba zer w zapisie dziesiętnym potęgi 1000¹⁰⁰⁰ .
21. Najmniejszy wspólny mianownik ułamków: \(\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6}\).

Gdyby miliard złotych w banknotach dziesięciozłotowych udało się ułożyć jeden banknot na drugim to powstałby stos o wysokości 10 km. Grubość banknotu dziesięciozłotowego wynosi

Dla pewnych liczb naturalnych a i b, wyrażeniem, które może przyjąć wartość 2016 jest

Pani Ania wyjechała do Krakowa o godzinie 8:00. Po pewnym czasie także do Krakowa wyjechał Pan Jan. Jechał tą samą trasą, ale dwa razy szybciej. W połowie drogi wyprzedził panią Anię i do Krakowa przyjechał o półtorej godziny wcześniej niż ona.

Liczba 2017 jest liczbą pierwszą.

Ala ma kule o średnicy 2 cm i 6 cm wykonane z tego samego materiału.

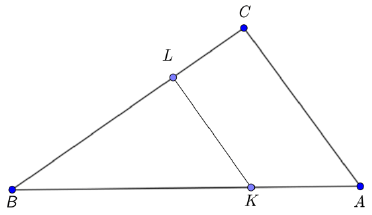
Dany jest trójkąt ABC o polu S oraz punkty K, L położone odpowiednio na bokach AB i BC takie, że |AK|:|KB|= 1:3 i |BL|:|LC|=3:1.

Dane są dwie liczby dwucyfrowe takie, że w pierwszej cyfra dziesiątek jest o 2 większa od cyfry jedności, a druga składa się z tych samych cyfr, ale zapisanych w odwrotnej kolejności. Jeżeli od pierwszej liczby odejmiemy drugą, to otrzymamy 18. Znajdź te pary liczb.

Dane są dwa prostokąty o wymiarach 20cm x 40cm. Jeden z nich jest powierzchnią boczną graniastosłupa prawidłowego czworokątnego, a drugi powierzchnią boczną walca. Oblicz objętości opisanych brył i wskaż tę spośród nich, która ma najmniejszą objętość.

W równoległoboku o kącie ostrym 60° odległości punktu przecięcia jego przekątnych od boków wynoszą 3cm i 5cm. Oblicz pole tego równoległoboku.

Narysuj w układzie współrzędnych pięciokąt wyznaczony przez osie układu i wykresy funkcji: y=4, y=-x+5, y=2x-4 . Oblicz pole tego pięciokąta.