Konkurs kuratoryjny z matematyki 2015/16 – Śląskie – Etap rejonowy

Rozwiąż krzyżówkę, wpisując w kratki odpowiednie cyfry. Hasło w zacieniowanych kratkach wyraża przybliżone prawdopodobieństwo uzyskania „szóstki” w grze LOTTO.

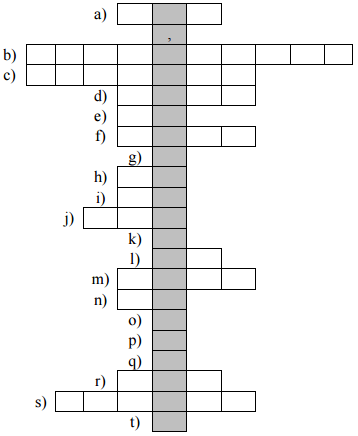
1. Długość boku trójkąta równobocznego o wysokości \(50\sqrt{3}\) .
2. Milion tysięcy.
3. Spośród liczb: 1111002, 1111004, 1111008, liczba podzielna przez 12.
4. Dzielna w ilorazie \(\frac{1020}{3040}\) .
5. Liczba zer w wyniku działania \(\frac{{{\left( {{1000}^{2}} \right)}^{10}}}{{{10}^{8}}\cdot {{10}^{12}}}\).
6. Liczba przeciwna do największej czterocyfrowej liczby ujemnej.
7. Suma liczb, których nie można wstawić w miejsce x w wyrażeniu \(\frac{\sqrt[3]{x-2}}{{{x}^{2}}-9}\) .
8. Długość boku trójkąta równobocznego o polu \(625\sqrt{3}\) .
9. Sześcian najmniejszej nieparzystej liczby pierwszej.
10. Najmniejsza trzycyfrowa liczba pierwsza.
11. Skala podobieństwa, w której sześcian o polu powierzchni 600j² jest podobny do sześcianu o polu powierzchni 24j².
12. Wysokość walca o polu powierzchni całkowitej równej 750π i polu podstawy równej 225π.
13. Mianownik liczby odwrotnej do 11,11.
14. Wykładnik n w wyrażeniu 5^n-1⋅5ⁿ⋅5ⁿ⁺¹=5³⁶.
15. Wspólny dzielnik liczb 9, 24, 60, który jest liczbą pierwszą.
16. Wartość wyrażenia \(\sqrt{20-1+27:3\cdot 5}\) .
17. Miejsce zerowe funkcji y=-2x+8.
18. Średnia arytmetyczna liczb: 121, 122, 123, 124,125, 126, 127.
19. Przybliżenie liczby 777999 z dokładnością do setek.
20. Wartość wyrażenia \(\frac{\sqrt[3]{128}}{\sqrt[3]{2}}:\frac{\sqrt{28}}{\sqrt{7}}\).

W dany okrąg wpisano prostokąt, którego przekątne tworzą kąt o mierze 30º. Prowadzimy styczne do okręgu w wierzchołkach prostokąta.

Dane jest pudełko w kształcie sześcianu o krawędzi długości 15 cm. W pudełku można zmieścić

Reszty z dzielenia liczb a, b i c przez 5 są równe odpowiednio 1, 2 i 3.

Cenę towaru, która wyraża się liczbą całkowitą, podwyższono o 9 zł. Aby zapisać nową cenę, należy zamienić kolejność cyfr pierwotnej ceny.

Funkcja f przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą.

W pewnej klasie 20% uczniów otrzymało ocenę bardzo dobrą, 40% – ocenę dobrą, 6 uczniów – ocenę dostateczną, a pozostali otrzymali ocenę dopuszczającą. Nikt nie otrzymał oceny celującej ani niedostatecznej. Średnia wszystkich ocen tej klasy wynosi 3,7.

Na szczyt pewnej góry prowadzi 5 różnych szlaków: czarny, żółty, czerwony, niebieski i zielony. Turysta wybrał losowo drogę na szczyt i także losowo drogę powrotną.

W autobusie podróżuje 36 osób. Wśród pasażerów tego autobusu

Dwaj trenerzy przeprowadzili 6 szkoleń, z których pierwsze 3 prowadzili wspólnie. Pierwszy trener przeprowadził 4 szkolenia, w których wzięły udział 84 osoby. Drugi trener przeprowadził 5 szkoleń, w których wzięło udział kolejno: 13, 21, 24, 20, 31 osób. Ile osób w sumie przeszkolili?

W trapezie równoramiennym przekątne przecinają się pod kątem prostym. Oblicz pole tego trapezu, jeżeli podstawy mają długości 20cm i 12cm.

Dany jest trapez ABCD niebędący równoległobokiem. Odcinki AB oraz CD są podstawami trapezu, a odcinek DE jest jego wysokością. Na odcinku DE wybrano punkt L o tej własności, że suma pól trójkątów ABL oraz CDL jest równa połowie pola trapezu ABCD. Uzasadnij, że punkt L dzieli odcinek DE na połowę.

Prom, płynąc pod wiatr, przebył pierwszą część trasy z pewną stałą prędkością. Pozostałą trasę przepłynął przy bezwietrznej pogodzie, także ze stałą prędkością, ale większą o 20% od poprzedniej. Gdyby całą drogę prom płynął z taką prędkością, jak w drugiej części trasy, to podróż trwałaby o 20 minut krócej. Oblicz, w jakim czasie prom pokonał pierwszą część trasy, gdy płynął pod wiatr.