Konkurs kuratoryjny z matematyki 2014/15 – Śląskie – Etap szkolny
Zobacz wszystkie zadania i rozwiązania wideo konkursu kuratoryjnego z matematyki 2014 – 2015 województwa śląskiego – etap szkolny.
Rozwiąż krzyżówkę. Hasło w zacieniowanych okienkach to przydomek włoskiego matematyka Leonarda z Pizy oraz tytuł książki, w której wprowadził on do matematyki europejskiej cyfry arabskie i pojęcie zera. Hasło nie jest oceniane, ale zweryfikuje Twoje odpowiedzi.
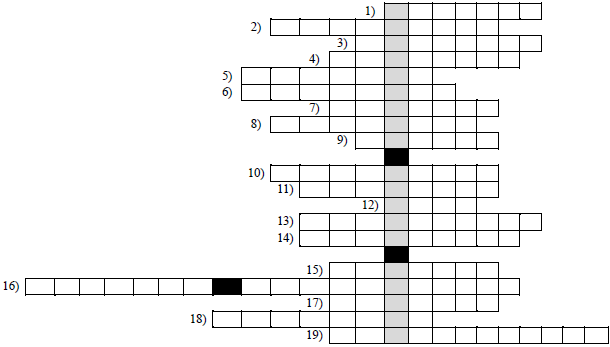
1. Każdemu argumentowi przyporządkowuje dokładnie jedną wartość.
2. Figura płaska mająca pięć boków.
3. Wyrażenie \({a^3}\) pozwala obliczyć jej wartość dla sześcianu o krawędzi długości a.
4. Kąt, którego ramiona zawierają promienie okręgu, to kąt…
5. Liczba naturalna, która ma więcej niż dwa dzielniki, to liczba…
6. Jeden z boków równoległych w trapezie.
7. Liczba w ułamku, która może być zerem.
8. Prostopadłościan mający wszystkie krawędzie równej długości.
9. Milion milionów.
10. Kąty o wspólnym ramieniu, których pozostałe ramiona dopełniają się do prostej, to kąty…
11. Jedna milionowa kilometra.
12. W trójkątach przystających odpowiednie mają równe długości.
13. Najmniejsza dwucyfrowa liczba pierwsza (słownie).
14. Jego prawdopodobieństwo dla wyrzucenia reszki w rzucie monetą symetryczną wynosi \(\frac{1}{2}\).
15. Jedna z 8 w ostrosłupie czworokątnym.
16. Wielokąt foremny o trzech bokach.
17. Wielokąt, który jest jednocześnie rombem i prostokątem.
18. Najdłuższa cięciwa okręgu.
19. System liczbowy o podstawie 10, to system…
- Można wskazać taką liczbę czterocyfrową, podzielną przez 3, której wszystkie cyfry są podzielne przez 3. PRAWDA/FAŁSZ
- Każda liczba pięciocyfrowa podzielna przez 3 ma wszystkie cyfry podzielne przez 3. PRAWDA/FAŁSZ
- Istnieje taka liczba sześciocyfrowa podzielna przez 3, w której żadna cyfra nie jest podzielna przez 3. PRAWDA/FAŁSZ
Na początku roku dziewczęta stanowiły \(46\frac{2}{3}\% \) wszystkich uczniów klasy. W ciągu roku z tej klasy odeszło 12,5% wszystkich chłopców.
- Na początku roku w klasie mogło być 30 uczniów. PRAWDA/FAŁSZ
- Na końcu roku liczba dziewcząt była taka sama jak liczba chłopców. PRAWDA/FAŁSZ
- Z klasy odeszło \(9\frac{2}{3}\% \) wszystkich uczniów. PRAWDA/FAŁSZ
Liczbami Fermata nazywamy liczby postaci \({2^{\left( {{2^n}} \right)}} + 1\), gdzie n jest liczbą naturalną. Liczbę wyznaczoną dla n oznaczamy symbolem \({F_n}\).
- Liczby \({F_0},{F_1},{F_2},{F_3}\) są liczbami pierwszymi. PRAWDA/FAŁSZ
- Liczba \({2^{64}} + 1\) jest liczbą Fermata. PRAWDA/FAŁSZ
- Liczba 19 jest liczbą Fermata. PRAWDA/FAŁSZ
Jeżeli a, b, c, d są liczbami dodatnimi takimi, że 3a = 5b, 6c = 5d i 2c = 7a, to prawdziwa jest nierówność:
- b < a < d PRAWDA/FAŁSZ
- c < d < b PRAWDA/FAŁSZ
- a < c < d PRAWDA/FAŁSZ
Jeżeli w pięciokącie wypukłym narysujemy wszystkie przekątne, to zawsze otrzymamy
- mniej niż 20 trójkątów. PRAWDA/FAŁSZ
- dokładnie 5 trapezów. PRAWDA/FAŁSZ
- dokładnie 20 czworokątów. PRAWDA/FAŁSZ
W okręgu podzielonym na 8 równych części poprowadzono cięciwy i otrzymano kąty \(\alpha ,\;\beta ,\;\gamma \) (jak pokazano na rysunku).
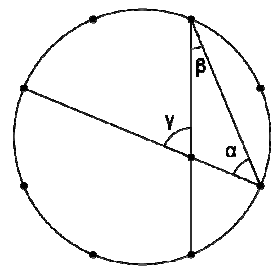
- \(\alpha = 45^\circ \) PRAWDA/FAŁSZ
- \(\alpha = 2\beta \) PRAWDA/FAŁSZ
- \(\gamma = \alpha + \beta \) PRAWDA/FAŁSZ
Każdy z boków kwadratu podzielono na 3 równe części i utworzono figurę F zacieniowaną na rysunku.
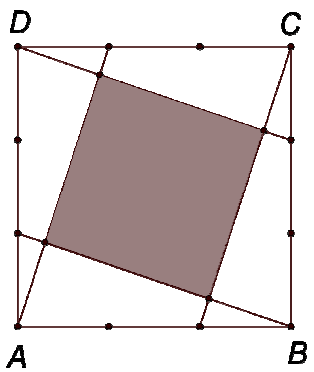
- Figura F jest równoległobokiem. PRAWDA/FAŁSZ
- Figura F jest rombem. PRAWDA/FAŁSZ
- Figura F nie jest kwadratem. PRAWDA/FAŁSZ
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Prawidłowo sformułowana cecha podzielności przez 4, to zdanie:
- Liczba jest podzielna przez 4, jeżeli jej dwie ostatnie cyfry są podzielne przez 4. PRAWDA/FAŁSZ
- Liczba jest podzielna przez 4, jeżeli jej dwie ostatnie cyfry tworzą liczbę podzielną przez 4. PRAWDA/FAŁSZ
- Liczba jest podzielna przez 4, jeżeli liczba jej setek jest podzielna przez 4. PRAWDA/FAŁSZ
Miejscowości X i Y są oddalone od siebie o 80 km. Statek wycieczkowy, płynąc z prądem rzeki z X do Y, pokonuje tę trasę w czasie 4 godzin, a płynąc z powrotem – w czasie 5 godzin. Oblicz prędkość statku oraz prędkość nurtu rzeki, zakładając, że statek płynie ze stałą prędkością oraz prędkość prądu rzeki też jest stała.
Treść dostępna po opłaceniu abonamentu.Iloczyn cyfr pewnej liczby trzycyfrowej wynosi 36, a suma jej cyfr jest równa 13. Podaj wszystkie takie liczby trzycyfrowe, które spełniają te warunki. Uzasadnij, że są to wszystkie takie liczby.
Treść dostępna po opłaceniu abonamentu.Na rysunku przedstawiono kwadrat ABCD i trójkąt CEO. Punkt O jest środkiem symetrii tego kwadratu. Pole trójkąta CEO stanowi \(\frac{1}{{20}}\) pola kwadratu. Oblicz, jaką część długości boku kwadratu ABCD stanowi długość boku CE trójkąta.
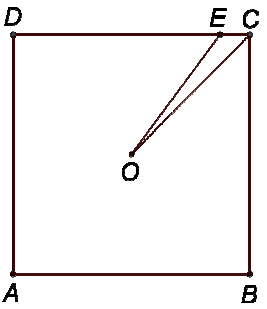 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Objętość prostopadłościanu wynosi \(405\,c{m^3}\). Stosunek długości krawędzi wychodzących z jednego wierzchołka wynosi 1 : 3 : 5. Oblicz pole powierzchni tego prostopadłościanu.
Treść dostępna po opłaceniu abonamentu.Losując bez zwracania dwie liczby spośród następujących: 0, 1, 2, 3, 4, 5, 6, 7, 8, możemy otrzymać 36 różnych wyników (wynik losowania {a, b} i {b, a} jest tym samym wynikiem). Oblicz prawdopodobieństwo, że różnica między większą a mniejszą z wylosowanych liczb jest większa od 4.
Treść dostępna po opłaceniu abonamentu.



