Konkurs kuratoryjny z matematyki 2013/14 – Śląskie – Etap szkolny

Rozwiąż krzyżówkę. Hasło, którym jest imię i nazwisko znanego polskiego matematyka i kryptologa oraz nazwa urządzenia, którego działanie pomógł rozszyfrować, odczytasz w zacieniowanych okienkach. Nie jest ono oceniane, ale zweryfikuje Twoje odpowiedzi.

1. 10⁶ milimetrów.
2. Liczba n w potędze aⁿ.
3. Czworokąt, który ma wszystkie boki równej długości.
4. Milion milionów.
5. Kąt o mierze większej niż 90° i mniejszej niż 180°.
6. Równość dwóch wyrażeń algebraicznych.
7. Punkt wspólny dwóch ramion kąta.
8. Przekształcenie geometryczne: … osiowa, … środkowa.
9. Argument funkcji, dla którego przyjmuje ona wartość zero.
10. Odcinek łączący środek koła z punktem okręgu.
11. Dzielnik w ułamku.
12. Liczba oznaczająca położenie punktu na osi liczbowej.
13. Odcinek łączący dwa niekolejne wierzchołki wielokąta wypukłego.
14. Dziesiąta część procenta.
15. Liczba, od której odejmujemy.
16. Każda z liczb w mnożeniu.
17. Prosta, która ma dwa punkty wspólne z okręgiem.
18. Zbiór punktów płaszczyzny.
19. Bok trapezu niebędący podstawą.
20. Czworokąt, który ma dwie przekątne wzajemnie prostopadłe, tej samej długości.

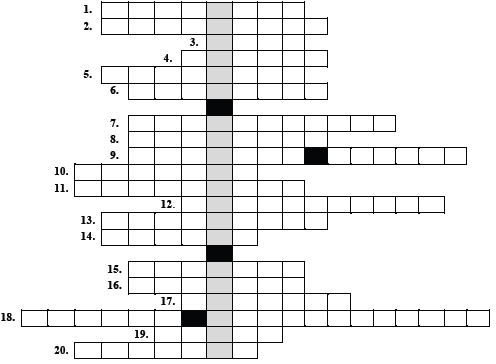
Diagram kołowy przedstawia procentowy udział produkcji pewnego artykułu w kolejnych miesiącach półrocza.

1. W trzecim miesiącu produkcja wyniosła 200% produkcji w drugim miesiącu. PRAWDA/FAŁSZ
2. W piątym miesiącu, w stosunku do czwartego miesiąca, produkcja wzrosła o 25%. PRAWDA/FAŁSZ
3. Między 4. i 6. miesiącem wielkość produkcji wzrosła tyle razy, ile między 1. i 3. miesiącem. PRAWDA/FAŁSZ

Rozwiązanie:

Liczby p i q są różnymi liczbami pierwszymi.

1. Iloczyn p i q jest liczbą pierwszą. PRAWDA/FAŁSZ
2. Suma p i q może być liczbą pierwszą. PRAWDA/FAŁSZ
3. Iloraz p i q może być liczbą naturalną. PRAWDA/FAŁSZ

Rozwiązanie:

I.

Jeśli p jest liczbą pierwszą to ma dwa dzielniki 1 i p.
(p ∙ q) ma 4 dzielniki 1, p, q,p ∙ q, zatem (p ∙ q) nie jest liczbą pierwszą.Odpowiedź: FAŁSZ.

II.

Liczby: 2 i 3 są pierwsze, a ich suma 5 też jest liczbą pierwszą. Odpowiedź: PRAWDA.

III.

Ułamek \(\frac{p}{q}\) może być naturalny, jeśli licznik p jest wielokrotnością q, wówczas p skraca się z q. Wiemy jednak, że p jest pierwsze, zatem nie może być wielokrotnością liczby q. Odpowiedź: FAŁSZ.

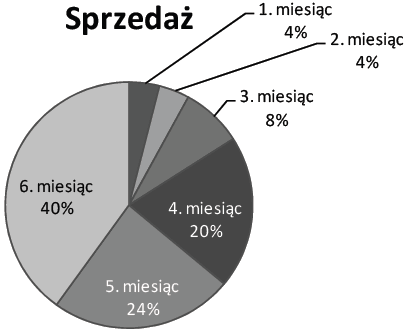
Liczba 5 jest rozwiązaniem równania:

1. x²=25. PRAWDA/FAŁSZ
2. \(\frac{1}{1-5}=1\). PRAWDA/FAŁSZ
3. \(\sqrt{5-x}=0\). PRAWDA/FAŁSZ

Rozwiązanie:

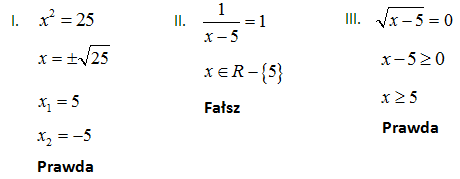
Pewien czworokąt ma dwie pary boków tej samej długości, a jego przekątne przecinają się pod kątem prostym. Tym czworokątem może być

1. prostokąt. PRAWDA/FAŁSZ
2. równoległobok. PRAWDA/FAŁSZ
3. deltoid. PRAWDA/FAŁSZ

Rozwiązanie:

W pkt. I zauważamy, że prostokąt może być kwadratem zatem ma boki parami równe, a przekątne przecinają się pod kątem prostym. Odpowiedź: Prawda.

W pkt. II zauważamy, że równoległobok może być kwadratem lub rombem zatem ma boki parami równe, a przekątne przecinają się pod kątem prostym w tym szczególnym przypadku. Odpowiedź: Prawda.

Deltoid – inaczej „latawiec” ma boki parami równe, a przekątne przecinają się pod kątem prostym. Odpowiedź: Prawda.

Każdą liczbę trójkątną można przedstawić w postaci sumy kolejnych, początkowych liczb naturalnych: T_n=1+2+…+n

1. Dziesiąta liczba trójkątna jest wielokrotnością liczby 11. PRAWDA/FAŁSZ
2. Suma siódmej i ósmej liczby trójkątnej jest podzielna przez 16. PRAWDA/FAŁSZ
3. Każdą liczbę trójkątną można zapisać w postaci \(T_{n}=\frac{n\big(n+1\big)}{2}\). PRAWDA/FAŁSZ

Rozwiązanie:

III.

Zaczniemy od końca tak będzie łatwiej.

Wyprowadzenie algebraiczne wzoru na n-tą liczbę trójkątną:

Graficzne wyprowadzenie wzoru na n-tą liczbę trójkątną:

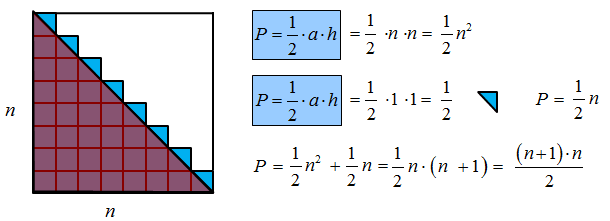
II.

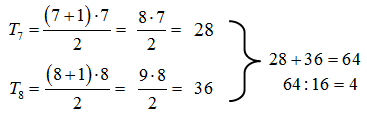
III.

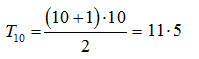
Liczba 2¹+2²+2³+…+2⁵⁰ jest podzielna przez

1. 2. PRAWDA/FAŁSZ
2. 3. PRAWDA/FAŁSZ
3. 6. PRAWDA/FAŁSZ

Rozwiązanie:

Na początku warto zauważyć, że jeśli liczba jest podzielna przez 2 i 3 to jest podzielna przez 6 i odwrotnie.

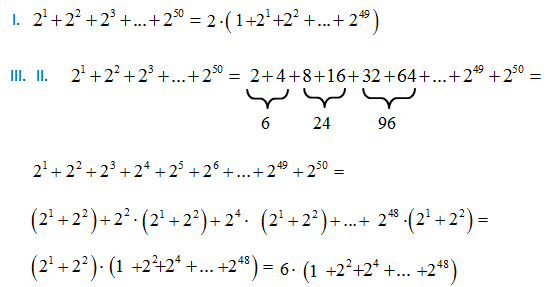
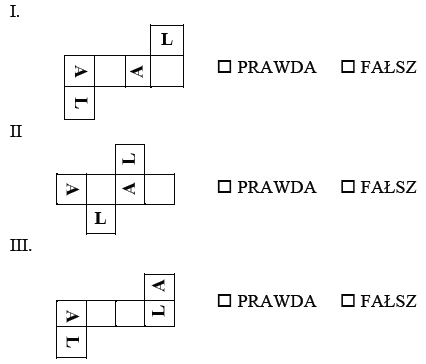
Na czterech bocznych ścianach sześcianu widnieje słowo LALA. Model takiego sześcianu można zbudować z siatki:

Z cyfr 0, 2, 3, 4 utworzono wszystkie możliwe liczby czterocyfrowe, przy czym w poszczególnych liczbach każda z cyfr występuje tylko raz. Wśród tych liczb

1. są 24 liczby podzielne przez 2. PRAWDA/FAŁSZ
2. jest 18 liczb podzielnych przez 3. PRAWDA/FAŁSZ
3. jest 6 liczb podzielnych przez 5. PRAWDA/FAŁSZ

Pręt o długości 110 cm podzielono na trzy części o długościach a, b, c, w taki sposób, że b jest 3 razy większe od a, c jest równe sumie połowy a i jednej trzeciej b. Oblicz długości: a, b, c.

Próba złota, to wskaźnik określający zawartość złota w stopie. Wyraża się go w promilach, np. jeśli stop zawiera 50% czystego złota, jest ono próby 500. Jaką masę stopu próby 960 należy dodać do 0,84 kg stopu próby 500, aby otrzymać stop próby 750?

Z pięciu kostek do gry jedna jest fałszywa, różni się od pozostałych masą. Przedstaw sposób ustalenia, czy kostka fałszywa jest cięższa czy lżejsza od prawdziwej. Można wykonać dwa ważenia na wadze szalkowej bez odważników.

Dany jest trójkąt ostrokątny ABC, w którym długość odcinka AB jest równa 10 cm. Na wysokości opuszczonej z wierzchołka C znajduje się punkt D taki, że odcinek CD ma długość 6 cm. Wykonaj odpowiedni rysunek i oblicz pole czworokąta ADBC.

Jeden z boków prostokąta ma długość 12 cm, a przekątna 13 cm. Przekątna podzieliła prostokąt na dwa trójkąty. W każdy z nich wpisano okrąg. Oblicz odległość między środkami tych okręgów.