Konkurs kuratoryjny z matematyki 2012/13 – Śląskie – Etap rejonowy

Rozwiąż krzyżówkę, wpisując w odpowiednie miejsca liczby opisane w pytaniach. Jeżeli liczba zawiera inne znaki niż cyfry, to zostały one dopisane, a Twoim zadaniem jest wpisanie jedynie cyfr. Zaznaczone pola rozwiązanej krzyżówki zawierają kolejne cyfry rozwinięcia dziesiętnego liczby \(\Phi \), tzw. „złotej liczby”.

a) Skala podobieństwa, w której kwadrat o polu 36 j² jest podobny do kwadratu o polu 49j².

b) Największa ujemna liczba trzycyfrowa.

c) Liczba odwrotna do 0,125.

d) Największy wspólny dzielnik liczb 630 i 420.

e) Mianownik najmniejszej z wymienionych liczb: \(-\frac{1}{9};-\frac{1}{7};-\frac{1}{5};-\frac{1}{3}.\)

f) Liczba \(\pi \) z dokładnością do 0,01.

g) Liczba zer w zapisie liczby jeden miliard.

h) Spośród liczb 512125, 858585, 321321 podzielna przez 15 jest liczba…

i) Sześcian parzystej liczby pierwszej.

j) Największa dwucyfrowa liczba pierwsza.

k) Wartość liczby: \({{2}^{\left( 3-2+1 \right)}}\)

l) Liczba naturalna, której nie można wstawić za x w wyrażeniu: \(\frac{1}{81-{{x}^{2}}}\)

m) Dzielnik w ilorazie: \(\frac{4321}{8765}\)

n) Wartość wyrażenia: \(\frac{\sqrt{243}}{\sqrt{3}}\)

o) Objętość ostrosłupa o takiej samej podstawie i wysokości, jaką ma graniastosłup o objętości 735 j³.

p) Wartość współczynnika b funkcji liniowej y = 2x – b , dla której liczba 242 jest miejscem zerowym tej funkcji.

q) Pole powierzchni kuli, której pole przekroju zawierającego środek tej kuli wynosi 120 j².

r) Wartość współczynnika przy x funkcji liniowej, której wykres jest równoległy do wykresu funkcji \(y=\frac{4}{5}x+1.\)

s) Wykładnik n w wyrażeniu \({{8}^{4}}={{2}^{n}}\)

t) Przybliżenie liczby 99555 z dokładnością do tysięcy.

Jeżeli 10 pomp w ciągu dziesięciu minut wypompowuje 10 ton wody, to

1. 25 pomp wypompowuje 25 ton wody w ciągu 10 minut. PRAWDA/FAŁSZ
2. 5 pomp wypompowuje 10 ton wody w ciągu 20 minut. PRAWDA/FAŁSZ
3. 10 pomp wypompowuje 5 ton wody w ciągu 5 minut. PRAWDA/FAŁSZ

W pewnym miesiącu trzy niedziele wypadły w dni parzyste.

1. Dwudziesty tego miesiąca wypada w piątek. PRAWDA/FAŁSZ
2. Trzydziesty tego miesiąca wypada w niedzielę. PRAWDA/FAŁSZ
3. Poniedziałków w tym miesiącu musi być 5. PRAWDA/FAŁSZ

Liczba n nazywa się średnią harmoniczną liczb a i b, jeżeli \(\frac{2}{n}=\frac{1}{a}+\frac{1}{b}.\)

1. Średnia harmoniczna liczb przeciwnych jest równa 0. PRAWDA/FAŁSZ
2. Jeżeli średnia harmoniczna liczb a i b jest równa ich średniej arytmetycznej, to a = b. PRAWDA/FAŁSZ
3. Średnia harmoniczna liczb odwrotnych jest odwrotnością ich średniej arytmetycznej. PRAWDA/FAŁSZ

Dla dowolnej liczby naturalnej n

1. \({{2}^{n-1}}+{{2}^{n-1}}+{{2}^{n-1}}+{{2}^{n-1}}={{2}^{4n-4}}\) PRAWDA/FAŁSZ
2. \({{5}^{n-1}}+{{5}^{n-1}}+{{5}^{n-1}}+{{5}^{n-1}}+{{5}^{n-1}}={{5}^{n}}\) PRAWDA/FAŁSZ
3. \({{6}^{n-1}}+{{6}^{n-1}}+{{6}^{n-1}}+{{6}^{n-1}}+{{6}^{n-1}}+{{6}^{n-1}}={{6}^{6n}}\)PRAWDA/FAŁSZ

Działanie \(\otimes \) dla liczb rzeczywistych określono następującym wzorem: a\(\otimes \) b = a + b+ a\(\cdot \)b. Wtedy:

1. a\(\otimes \)0 = a . PRAWDA/FAŁSZ
2. 6\(\otimes \) (-6)= 0 .PRAWDA/FAŁSZ
3. (a-1) \(\otimes \) (a+1) = (a\(\otimes \)a)-1. PRAWDA/FAŁSZ

Na planie sporządzonym w skali 1 : 2000 plac ma kształt kwadratu o polu 225 cm².

1. Obwód tego placu w rzeczywistości wynosi 1200 m. PRAWDA/FAŁSZ
2. Pole tego placu w rzeczywistości przekracza 10 ha. PRAWDA/FAŁSZ
3. Pole placu na planie wykonanym w skali 1 : 5000 wynosi 90 cm². PRAWDA/FAŁSZ

Dane jest wyrażenie \(W=\frac{2n+15}{n}.\)

1. Istnieje liczba parzysta n, dla której wyrażenie W przyjmuje wartość będącą liczbą naturalną. PRAWDA/FAŁSZ
2. Istnieją dokładnie 4 liczby naturalne n, dla których wyrażenie W przyjmuje wartość będącą liczbą naturalną. PRAWDA/FAŁSZ
3. Istnieje liczba całkowita n, dla której wartość wyrażenia W wynosi zero. PRAWDA/FAŁSZ

Funkcja F określona jest w następujący sposób: każdej liczbie rzeczywistej x spełniającej warunek –3 ≤ x ≤ 3 funkcja przyporządkowuje największą liczbę całkowitą, nie większą niż x.

1. Funkcja F jest funkcją rosnącą. PRAWDA/FAŁSZ
2. Najmniejszą wartością tej funkcji jest liczba –3. PRAWDA/FAŁSZ
3. Dla każdej liczby x spełniającej warunek 0 ≤ x < 1 funkcja przyjmuje wartość zero. PRAWDA/FAŁSZ

Ania w ciągu godziny pokonała rowerem trasę o długości 10,5 km. Na pierwszym odcinku trasy biegnącej ścieżką rowerową, średnia prędkość jazdy Ani wynosiła 18 km/h, a na drugim, prowadzącym przez las 8 km/h. Oblicz, który odcinek trasy był dłuższy – pierwszy (na ścieżce rowerowej) czy drugi (przez las)?

Cena biletu na mecz wynosiła 45 zł. Gdy cenę obniżono, okazało się, że na mecz przychodzi o 50% widzów więcej, a dochód ze sprzedaży biletów wzrósł o 25%. O ile obniżono cenę biletu?

Dwie ściany prostopadłościanu o wspólnej krawędzi długości 15 cm są prostokątami podobnymi w skali k = 1,5. Oblicz pole powierzchni i objętość tej bryły.

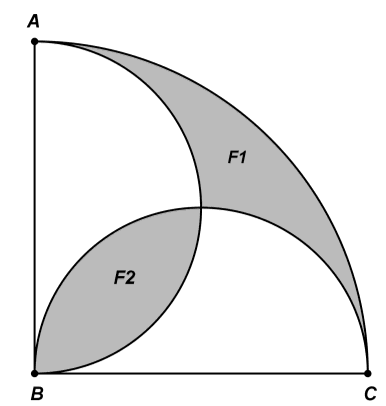
W ćwiartkę koła wpisano półkola, jak pokazano na rysunku. Wykaż, że pola figur \({{F}_{1}}\ i\ {{F}_{2}}\) są równe.