Konkurs kuratoryjny z matematyki 2011/12 – Śląskie – Etap wojewódzki
Rozwiąż krzyżówkę. Zaznaczone pola rozwiązanej krzyżówki zawierają nazwę trzynastokąta foremnego. Kompletne hasło krzyżówki jest oceniane dodatkowo 1 punktem.
a) Kwadrat ma …. osie symetrii.
b) Inna nazwa ostrosłupa trójkątnego.
c) Może być naturalna, całkowita i nie tylko.
d) Bryła, której podstawą jest wielokąt, a ściany boczne są trójkątami o jednym wspólnym wierzchołku.
e) Każda z dwóch części, na jakie dzielą okrąg dwa różne punkty należące do tego okręgu.
f) Bryła obrotowa powstała na skutek obrotu prostokąta wokół jednego boku.
g) Największa liczba jednocyfrowa.
h) Wartość środkowa dla nieparzystej liczby danych uporządkowanych od najmniejszej do największej.
i) Bryła powstała przez obrót trójkąta równoramiennego wokół jego osi symetrii.
j) Przyporządkowanie, w którym każdemu elementowi jednego zbioru odpowiada dokładnie jeden element drugiego zbioru.
k) Czworokąt, który ma jedną parę boków równoległych.
l) Zbiór punktów równoodległych od jednego ustalonego punktu.
m) Odcinek prostopadły do prostej zawierającej jeden z boków trójkąta, którego jeden koniec należy do tej prostej, a drugi jest przeciwległym wierzchołkiem trójkąta.
n) Odcinek łączący punkty okręgu i zawierający środek okręgu.
Znajdź cyfry A, B, C, dla których poprawny jest zapis:
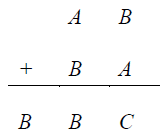 Odp.: A = ….., B = ….., C = ….
Odp.: A = ….., B = ….., C = ….
Wartość wyrażenia \(\frac{\frac{1}{3}\cdot \sqrt[3]{-27}+{{3}^{2}}}{{{3}^{2}}}\) jest równa:
- \(\frac{1}{3}\sqrt[3]{-27}\) PRAWDA/FAŁSZ
- \(\frac{-1+{{3}^{2}}}{{{3}^{2}}}\)PRAWDA/FAŁSZ
- \(\frac{-8}{9}\) PRAWDA/FAŁSZ
Suma długości boku kwadratu i jego przekątnej wynosi 1 dm.
- Pole tego kwadratu jest równe \(\frac{1}{3+2\sqrt{2}}d{{m}^{2}}.\) PRAWDA/FAŁSZ
- Obwód tego kwadratu wynosi \(\frac{4}{1+\sqrt{2}}dm. \) PRAWDA/FAŁSZ
- Przekątna tego kwadratu ma długość \(\frac{\sqrt{2}}{1+\sqrt{2}}dm. \) PRAWDA/FAŁSZ
Uczniowie klasy I planują wycieczkę. Gdyby każdy z nich wpłacił po 13 zł, do pokrycia kosztów zabrakłoby 57 zł, natomiast gdyby każdy wpłacił po 15 zł, to po opłaceniu kosztów zostałoby 5 zł.
- Koszt wycieczki wynosi 500 zł. PRAWDA/FAŁSZ
- Na wycieczkę zamierzało pojechać 31 uczniów.PRAWDA/FAŁSZ
- Nie można określić liczby uczniów, którzy zamierzali pojechać na wycieczkę ani kosztów wycieczki. PRAWDA/FAŁSZ
Na rysunku poniżej przedstawiono prostą zasadę utworzenia z patyczków pewnego ciągu figur.
- Dwudziesta figura w tym ciągu składa się ze 120 patyczków. PRAWDA/FAŁSZ
- Z 50 patyczków można ułożyć ciąg składający się z 4 takich figur. PRAWDA/FAŁSZ
- Do utworzenia ciągu składającego się z ośmiu figur wystarczy 200 patyczków. PRAWDA/FAŁSZ
Dla dowolnych liczb x, y funkcja f spełnia warunki: f(ax) = af(x) oraz f(x+y) = f(x) + f(y). Jeżeli f(2) = 6 i f(3) = 9, to:
- f (4) = 12 PRAWDA/FAŁSZ
- f (5) = 15 PRAWDA/FAŁSZ
- f (8) = 26 PRAWDA/FAŁSZ
Liczba przekątnych wielokąta wypukłego , który ma n boków i n ≥ 3 wyraża się wzorem \(\frac{n\cdot \left( n-3 \right)}{2}.\)
- Trzynastokąt ma pięć razy więcej przekątnych niż boków. PRAWDA/FAŁSZ
- Każdy wielokąt wypukły o nieparzystej liczbie boków ma nieparzystą liczbę przekątnych. PRAWDA/FAŁSZ
- W n-kącie liczba przekątnych wyprowadzonych z jednego wierzchołka jest równa (n – 3) . PRAWDA/FAŁSZ
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
W kongresie matematycznym brało udział 100 naukowców: 90 z nich władało językiem angielskim, 75 – językiem niemieckim, 70 – językiem francuskim, 66 – językiem rosyjskim.
- Językiem niemieckim i francuskim posługiwało się co najmniej 45 osób. PRAWDA/FAŁSZ
- Językiem angielskim ani niemieckim nie władało co najwyżej 15 osób. PRAWDA/FAŁSZ
- Językiem rosyjskim i francuskim mówiło co najwyżej 66 uczestników. PRAWDA/FAŁSZ
W urnie znajduje się dwa razy więcej losów przegrywających niż wygrywających. Wyciągamy jeden los.
- Prawdopodobieństwo wylosowania losu przegrywającego wynosi 0,5. PRAWDA/FAŁSZ
- Prawdopodobieństwo wylosowania losu wygrywającego wynosi 0,(3). PRAWDA/FAŁSZ
- Prawdopodobieństwo wylosowania losu wygrywającego jest dwa razy mniejsze niż prawdopodobieństwo losu przegrywającego. PRAWDA/FAŁSZ
W meczu koszykówki najlepszy zawodnik zdobył 26 punktów. Stosunek wykonanych przez niego celnych rzutów za 3 punkty, za 2 punkty i za 1 punkt (rzuty osobiste) wyniósł 2:3:1.
- Koszykarz oddał 6 celnych rzutów za 2 punkty. PRAWDA/FAŁSZ
- Koszykarz zdobył 12 punktów celnymi rzutami za 3 punkty. PRAWDA/FAŁSZ
- Koszykarz oddał 3 rzuty osobiste. PRAWDA/FAŁSZ
Dwa sześciokąty foremne są podobne w skali 1:6. Suma ich pól jest równa \(222\sqrt{3}c{{m}^{2}}.\) Oblicz pole i obwód każdego sześciokąta foremnego.
Treść dostępna po opłaceniu abonamentu.Podstawa trójkąta ma długość \(4+4\sqrt{3}\), a kąty do niej przylegające mają miary \(60{}^\circ \ i\ 45{}^\circ .\) Oblicz obwód tego trójkąta.
Treść dostępna po opłaceniu abonamentu.Trójkąt równoboczny o bokach 12 cm jest siatką czworościanu foremnego. Oblicz objętość tego czworościanu.
Treść dostępna po opłaceniu abonamentu.



