Konkurs kuratoryjny z matematyki 2010/11 – Śląskie – Etap szkolny
Zobacz wszystkie zadania i rozwiązania wideo konkursu kuratoryjnego z matematyki 2010 – 2011 województwa śląskiego – etap szkolny.
W trapezie równoramiennym ABCD przekątne AC i BD przecinają się w punkcie O. Wtedy:
- Pola trójkąta AOD i trójkąta BOC są równe. PRAWDA/FAŁSZ
- Obwody i pola trójkąta ABD i trójkąta ABC są równe. PRAWDA/FAŁSZ
- Pola trójkąta ABO i trójkąta COD są równe. PRAWDA/FAŁSZ
Uczniowie na lekcji wychowania fizycznego ustawili się w szeregu. Wiadomo, że:
D stoi pomiędzy E i F,
C stoi pomiędzy D i E,
B stoi pomiędzy C i D,
A stoi pomiędzy B i C.
Oceń poniższe stwierdzenia:
- Bezpośrednimi sąsiadami A są E i F. PRAWDA/FAŁSZ
- A może stać na trzeciej pozycji z lewej strony. PRAWDA/FAŁSZ
- A może stać na czwartej pozycji z lewej strony. PRAWDA/FAŁSZ
Mieszkaniec pewnej miejscowości wysłuchał dwóch prognoz pogody. W prognozie radiowej dla Zakopanego podano, że spadnie tam w ciągu najbliższej doby 40 litrów wody ma metr kwadratowy. W prognozie telewizyjnej dla Kołobrzegu zapowiedziano opady wielkości 40 mm (opad mierzony wysokością warstwy wody).
- Prognoza przewidywała większe opady w Kołobrzegu. PRAWDA/FAŁSZ
- Prognoza przewidywała większe opady w Zakopanem. PRAWDA/FAŁSZ
- Obie prognozy przewidywały ten sam poziom opadów. PRAWDA/FAŁSZ
Warunek x > y spełniony jest gdy:
- \(x=\frac{1}{5};\quad y=\frac{3}{14}\) PRAWDA/FAŁSZ
- \(x={{10}^{20}};\quad y={{90}^{10}}\) PRAWDA/FAŁSZ
- \(x=2\sqrt{5};\quad y=3\sqrt{2}\) PRAWDA/FAŁSZ
Rysunek przedstawia siatkę sześcianu:
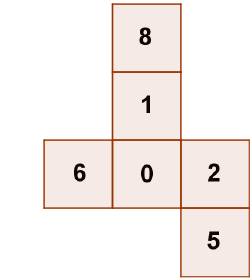
- Średnia arytmetyczna liczb na ścianach sześcianu wynosi 4,4. PRAWDA/FAŁSZ
- Wszystkich dwucyfrowych liczb utworzonych z cyfr umieszczonych na przeciwległych ścianach sześcianu jest 5. PRAWDA/FAŁSZ
- Suma kwadratów liczb na przeciwległych ścianach sześcianu jest zawsze podzielna przez 4. PRAWDA/FAŁSZ
Dla wszystkich liczb rzeczywistych a i b zachodzi warunek:
- \({{\left( a-b \right)}^{3}}={{\left( b-a \right)}^{3}}\) PRAWDA/FAŁSZ
- \(-{{a}^{3}}={{\left( -a \right)}^{3}}\) PRAWDA/FAŁSZ
- \({{\left( a+b \right)}^{2}}\ge {{a}^{2}}+{{b}^{2}}\) PRAWDA/FAŁSZ
Oceń poniższe stwierdzenia:
- 25% liczby \({{4}^{12}}\quad to\quad {{4}^{11}}\) PRAWDA/FAŁSZ
- 200% liczby \({{2}^{12}}\quad to\quad {{2}^{24}}\) PRAWDA/FAŁSZ
- Liczba o 100% większa od \({{2}^{12}}\quad to\quad {{2}^{13}}\) PRAWDA/FAŁSZ
Biegacz przebiegł ze stałą prędkością odcinek trasy z punktu A do punktu B. Po odpoczynku szedł ze stałą prędkością z B do A. Wykres przedstawia zależność drogi przebytej przez biegacza od czasu.
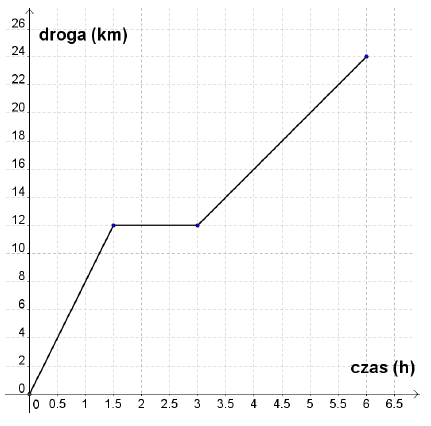
- Biegacz biegł z prędkością \(8\frac{km}{h}\). PRAWDA/FAŁSZ
- Biegacz szedł z prędkością \(4\frac{km}{h}\). PRAWDA/FAŁSZ
- Średnia prędkość na całej trasie wynosiła \(6\frac{km}{h}\). PRAWDA/FAŁSZ
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Uzasadnij, że iloczyn liczb: \(1\cdot 3\cdot 5\cdot 7\cdot …\cdot 2007\cdot 2009\cdot 2011\) jest podzielny przez 2013.
Treść dostępna po opłaceniu abonamentu.Gdyby zapisano obok siebie wszystkie numery stron książki znajdujące się na wszystkich stronach od 1. do 345., to z ilu cyfr składałaby się otrzymana liczba? Zapisz stosowne obliczenia i opisz tok rozumowania.
Treść dostępna po opłaceniu abonamentu.Na prostej obrano kolejno cztery punkty: A, B, C i D w ten sposób, że \(\left| AB \right|=6cm,\ \quad \left| AD \right|=10cm\quad oraz\quad \left| BC \right|=2cm.\) Po jednej stronie prostej narysowane są dwa półokręgi o średnicy AB i AC, a po drugiej stronie półokręgi o średnicy BD i CD. Oblicz pole obszaru ograniczonego półokręgami.
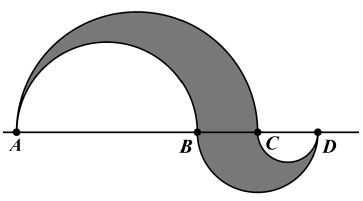 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Oblicz obwód i pole figury przedstawionej na rysunku.
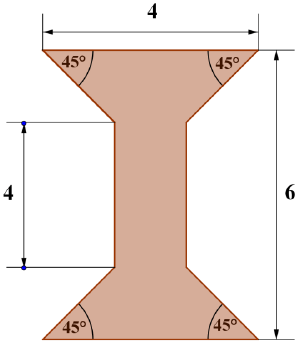 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.




