Konkurs kuratoryjny z matematyki 2009/2010 – Śląskie – Etap rejonowy
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP REJONOWY – 19 stycznia 2010 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 12 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie
- Przeczytaj dokładnie treść zadań, zwracając uwagę na to, czy polecenie nakazuje podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- W części I (zadania od 1 do 8) wpisz TAK lub NIE w kratce z lewej strony obok, każdej z trzech odpowiedzi. Za każdy poprawny wpis otrzymasz 1 punkt – w sumie, za każde z tych zadań, możesz otrzymać maksymalnie 3 punkty.
- Margines po prawej stronie kartki i ostatnia strona są przeznaczone na brudnopis.
- Notatki i obliczenia w brudnopisie nie podlegają ocenie.
- Zabronione jest korzystanie z kalkulatorów i korektorów pisma (ewentualne błędne zapisy należy wyraźnie skreślić).
- Na rozwiązanie wszystkich zadań masz 90 minut.
- Aby zakwalifikować się do finału musisz zdobyć co najmniej 34 punkty.
Plik z zadaniami z konkursu kuratoryjnego – etap rejonowy
Pobierz zadania matematyczne z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap rejonowy
W równoległoboku o bokach 6 i 15 pole wynosi \(45\sqrt{3}\). Prawdą jest, że:
Kierowca jechał najpierw 3 godziny z prędkością 80 km/h, a potem 2 godziny z prędkością 70 km/h. Prawdą jest, że:
Dana jest liczba 1092-92. Prawdą jest, że:
Punkty A(1;-2) i B(4;2) są dwoma wierzchołkami trójkąta równobocznego ABC. Prawdą jest, że:
S(n) oznacza sumę cyfr liczby naturalnej dodatniej. Prawdą jest, że:
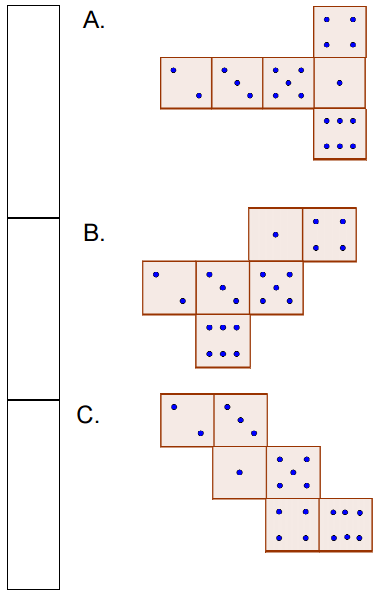
Kostki do gry wykonane są zgodnie z następującą zasadą: suma oczek na dwóch przeciwległych ściankach zawsze jest równa siedem. Oceń, z której z narysowanych poniżej siatek można złożyć kostkę spełniającą ten warunek.
Dany jest trójkąt prostokątny równoramienny ABC o ramieniu 2 cm. Z wierzchołka B kąta ostrego wykreślono okrąg o promieniu 2 cm tak, że przeciął przeciwprostokątną w punkcie D (jak na rysunku).
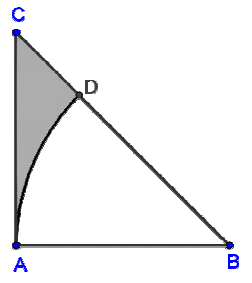
Prawdą jest, że
Alek, Basia, Cecylia i Darek mają razem 200 płyt CD. Alek posiada 27% wszystkich płyt, Basia 33%, Cecylia 37%, a pozostałe ma Darek. Prawdą jest, że:
II część konkursu kuratoryjnego z matematyki – zadania otwarte
Funkcja f określona jest na zbiorze liczb naturalnych dodatnich wzorem:
\[f\left( n \right)=\left\{ \begin{matrix}
n-3,\quad gdy\text{ }n\text{ }jest\text{ }liczba\text{ }nieparzysta\text{ } \\
\frac{1}{2}n,\quad gdy\text{ }n\text{ }jest\text{ }liczba\text{ }parzysta \\
\end{matrix} \right.\]
a) Oblicz f(10).
b) Wyznacz argumenty, dla których funkcja przyjmuje wartość zero.
c) Naszkicuj wykres funkcji dla n≤12 .
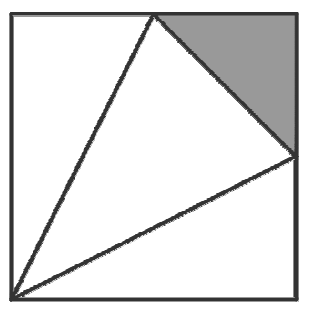
Kwadrat podzielono na trójkąty w taki sposób, jak na rysunku, (podstawą jest trójkąt zamalowany). Otrzymano siatkę ostrosłupa. Oblicz pole powierzchni całkowitej tego ostrosłupa, jeżeli jego objętość wynosi 9cm³.
Jeżeli każdy bok danego prostokąta zwiększymy o 2cm, to jego pole wzrośnie o 18cm². O ile cm² zmieni się pole danego prostokąta, jeżeli każdy jego bok zmniejszymy o 1cm?
Na pierwszym roku studiów, na kierunku budowa maszyn, kobiety stanowią 25% ogółu przyjętych. Gdyby w kolejnym roku liczba przyjętych pań wzrosła o 1/3, a liczba mężczyzn zmalała o 20, to kobiety stanowiłyby 1/3 ogółu studiujących na pierwszym roku. Oblicz, ile osób przyjęto na pierwszy rok tych studiów, oraz ilu jest wśród nich mężczyzn?




