Konkurs kuratoryjny z matematyki 2008/09 – Śląskie – Etap szkolny
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP SZKOLNY – 24 listopada 2008 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 13 zadań.
- Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj dokładnie treść zadań, zwracając uwagę na to, czy polecenie nakazuje podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- W części I (zadania od 1 do 8) wpisz TAK lub NIE obok każdej z trzech odpowiedzi.
- Za każdy poprawny wpis otrzymasz 1 punkt – w sumie za każde z tych zadań możesz otrzymać maksymalnie 3 punkty.
- Margines po prawej stronie kartki jest przeznaczony na brudnopis.
- Na rozwiązanie wszystkich zadań masz 90 minut.
- Aby zakwalifikować się do etapu rejonowego musisz zdobyć co najmniej 36 punktów.
Plik z zadaniami z konkursu kuratoryjnego – etap szkolny
Pobierz zadania z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap szkolny
Przekątna kwadratu jest o 1 dłuższa od bok tego kwadratu. Prawdą jest, że:
Jeśli a i b są liczbami całkowitymi i spełniony jest warunek \(\frac{1}{101}<\frac{a}{b}<\frac{1}{100}\), to liczby a i b mogą przyjmować wartości:
Długość jednego boku prostokąta skrócono o 10%, a drugiego wydłużono o 10% i w ten sposób otrzymano kwadrat. Boki prostokąta mogły mieć długości:
W rombie o boku długości a , kąt rozwarty ma miarę 5 razy większą, niż kąt ostry. Wówczas :
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma miar jest równa 180º. Prawdą jest, że:
Pociąg przejeżdża przez most długości 600 m. Od chwili gdy lokomotywa wjeżdża na most do momentu opuszczenia go przez ostatni wagon upływa 1 minuta. Pociąg mija przęsło mostu w ciągu 20 sekund. Prawdą jest, że:
Reszta z dzielenia liczby pierwszej przez 21 jest liczbą złożoną. Resztą tą może być liczba:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Średnia wieku jedenastu piłkarzy to 22 lata. Gdy jeden gracz otrzymał czerwoną kartkę i zszedł z boiska to średnia wieku pozostałych wyniosła 21 lat. Piłkarz, który opuścił boisko:
II część konkursu kuratoryjnego z matematyki – zadania otwarte
Firma wywierciła 10 metrową studnię. Za pierwszy metr odwiertu należy zapłacić 145 zł, a pozostałe 9 metrów kosztuje 1080 zł (firma za każdy następny metr odwiertu pobiera stałą opłatę). Ile należy zapłacić za studnię o głębokości 15 metrów?
Treść dostępna po opłaceniu abonamentu.Oblicz pole zacieniowanego obszaru, jeżeli odcinek AB ma długość 40. Wszystkie okręgi i półokręgi są styczne, a cała poniższa figura ma jedną oś symetrii.
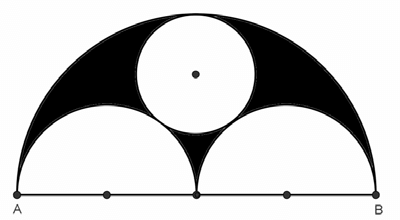Treść dostępna po opłaceniu abonamentu.
Pani Kowalska założyła lokaty w dwóch bankach. Pewną część ze swoich 40 000 zł złożyła w banku „X” na 8% w stosunku rocznym, a pozostałą kwotę w banku „Y” na 7% w stosunku rocznym. Po roku pani Kowalska otrzymała 42 551,50 po potrąceniu 19% podatku od zysku z lokaty ( każdy zysk z lokaty podlega opodatkowaniu podatkiem dochodowym w wysokości 19%) . Ile pieniędzy pani Kowalska wpłaciła do każdego banku?
Treść dostępna po opłaceniu abonamentu.Rozstrzygnij, czy liczba 100n+2-2008 jest podzielna przez 3, jeżeli n jest liczbą naturalną? Odpowiedź uzasadnij.
Treść dostępna po opłaceniu abonamentu.Wewnątrz trójkąta równobocznego o boku \(4\sqrt{3}\) wybrano dowolny punkt A. Oblicz sumę odległości punktu A od boków tego trójkąta.
Treść dostępna po opłaceniu abonamentu.