Konkurs kuratoryjny z matematyki 2007/2008 – Śląskie – Etap wojewódzki
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP WOJEWÓDZKI – 7 marca 2008 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 12 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj dokładnie treść zadań, zwracając uwagę na to, czy polecenie nakazuje podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie lub w inny sposób uzasadnić odpowiedź).
- W części I (zadania od 1 do 8) wpisz TAK lub NIE obok każdej z trzech odpowiedzi. Za każdy poprawny wpis otrzymasz 1 punkt – w sumie za każde z tych zadań możesz otrzymać maksymalnie 3 punkty.
- Margines po prawej stronie kartki jest przeznaczony na brudnopis.
- Zabronione jest korzystanie z kalkulatorów i korektorów pisma (ewentualne błędne zapisy należy wyraźnie skreślić).
- Na rozwiązanie wszystkich zadań masz 90 minut.
- Aby zastać laureatem musisz zdobyć co najmniej 36 punktów.
Plik z zadaniami z konkursu kuratoryjnego – etap wojewódzki
Pobierz zadania z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap wojewódzki
Spośród 5 kolejnych liczb nieparzystych co najmniej jedna dzieli się zawsze przez:
Z kwadratowego arkusza blachy o boku 10 cm wycina się możliwie największe koło, którego używa się do dalszej produkcji. Reszta blachy to odpady. Odpady stanowią:
Z liter składających się na słowo MATEMATYKA wybieramy losowo jedną literę, podobnie ze słowa KONKURS losujemy również jedną literę. Prawdą jest, że:
Czy prawidłowo porównano liczby?
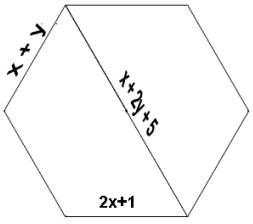
Dany jest sześciokąt foremny, w którym długości boków i jednej jego przekątnej można wyrazić za pomocą liczb dodatnich x i y, tak jak na rysunku:
Jeżeli f (x + 2) = 6x + 3 to:
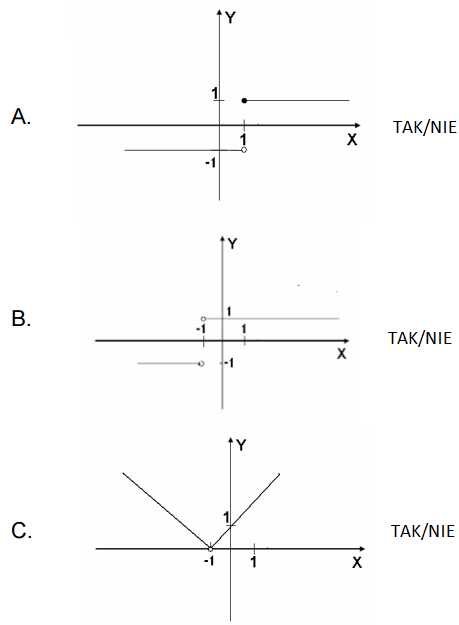
Wykresem funkcji \(f\left( x \right)=\frac{\left| x+1 \right|}{x+1}\) jest:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Do jednej ze ścian sześcianu o krawędzi długości 20 cm doklejono sześcian o krawędzi o połowę krótszej, a do ściany tego ostatniego kolejny sześcian znowu o krawędzi o połowę krótszej od poprzedniego. W przypadku każdej pary sklejonych ścian, środki ich przekątnych pokrywają się. Czy prawdą jest, że:
II część konkursu kuratoryjnego z matematyki – Zadania otwarte
Okrąg został podzielony na łuki w stosunku 5 : 9 : 10. Przez punkty podziału poprowadzono styczne do okręgu. Oblicz kąty trójkąta, którego wierzchołkami są punkty przecięcia opisanych stycznych.
Treść dostępna po opłaceniu abonamentu.Wiedząc, że \(\frac{a}{a+b}=\frac{1}{3}\) i a+b≠0 oblicz \(\frac{3b}{a+b}\):
Treść dostępna po opłaceniu abonamentu.Znajdź liczbę wiedząc, że suma jej cyfr wynosi 6 i ma dokładnie 4 dzielniki, których suma wynosi 192. Odpowiedź uzasadnij.
Treść dostępna po opłaceniu abonamentu.Rowerzysta obliczył, że jadąc z prędkością 12 km/h dojedzie na czas do miasta na mecz piłki nożnej. Po przebyciu 1/3 drogi popsuł mu się rower i naprawa trwała 20 minut. Żeby zdążyć na mecz, pozostałą część drogi musiał jechać z prędkością 15 km/h. Jaką drogę miał do przebycia rowerzysta?
Treść dostępna po opłaceniu abonamentu.



