Konkurs kuratoryjny z matematyki 2007/2008 – Śląskie – Etap rejonowy
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP REJONOWY – 31 stycznia 2008 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 14 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj dokładnie treść zadań, zwracając uwagę na to, czy polecenie nakazuje podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- W części I (zadania od 1 do 9) wpisz TAK lub NIE obok każdej z trzech odpowiedzi. Za każdy poprawny wpis otrzymasz 1 punkt – w sumie, za każde z tych zadań, możesz otrzymać maksymalnie 3 punkty.
- Margines po prawej stronie kartki jest przeznaczony na brudnopis.
- Zabronione jest korzystanie z kalkulatorów i korektorów pisma (ewentualne błędne zapisy należy wyraźnie skreślić).
- Na rozwiązanie wszystkich zadań masz 90 minut.
- Aby zakwalifikować się do finału musisz zdobyć co najmniej 41 punktów.
Plik z zadaniami z konkursu kuratoryjnego – etap rejonowy
Pobierz zadania z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap rejonowy
Setna cyfra po przecinku w zapisie dziesiętnym liczby \(\frac{14}{27}\) , to:
Równanie |2x+1|=5 ma następujące rozwiązania:
W klasie liczącej 31 osób dziewczęta stanowią mniej niż połowę, ale więcej niż jedną trzecią liczby wszystkich uczniów. W tej klasie może być:
Kasia zużywając równomiernie mydło w kształcie sześcianu zauważyła, że po 14 dniach wszystkie wymiary mydła zmniejszyły się o ½ swoich początkowych wartości. Jeżeli Kasia będzie zużywać mydło w tym samym tempie co dotychczas, to wystarczy go jej jeszcze na:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
W prostokącie przekątne o długości 10 cm przecinają się pod kątem 60°. Prawdą jest, że:
Liczba n(n+1)(n+2)(n+3) dla dowolnego naturalnego dzieli się przez:
W pewnej firmie jest ośmiu pracowników. Ich zarobki w złotych to: 1700, 1800, 2000, 2000, 2100, 2100, 2100 i 8000. Prawdą jest, że:
Kasia ma o 50% więcej pieniędzy niż Basia. O ile procent Basia ma mniej pieniędzy niż Kasia?
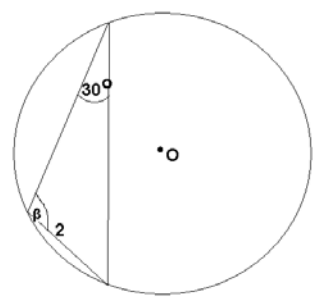
Dany jest okrąg opisany na trójkącie(tak jak na rysunku), w którym długość boku leżącego naprzeciw kąta 30° wynosi 2 cm. Prawdą jest, że:
II część konkursu kuratoryjnego z matematyki – etap rejonowy. Zadania otwarte.
Na szosie między dwoma przystankami odległymi od siebie o 2,8 km ustawiono dodatkowy przystanek w punkcie, który dzieli ten odcinek w stosunku 10:4. Jak daleko do nowego przystanku będzie miała osoba, która mieszka dokładnie pośrodku między starymi przystankami?
Treść dostępna po opłaceniu abonamentu.Narysuj wykres funkcji f, której dziedziną jest zbiór liczb całkowitych dodatnich mniejszych od 12 i f(n)=NWD(n;24). Wyznacz zbiór wartości tej funkcji. NWD(a;b) oznacza największy wspólny dzielnik liczb a i b.
Treść dostępna po opłaceniu abonamentu.Oblicz pole figury ograniczonej wykresami funkcji:
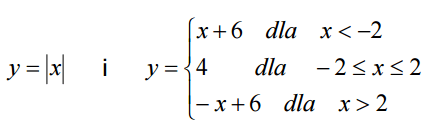Treść dostępna po opłaceniu abonamentu.
Konkurencyjne firmy A i B wypuściły na rynek sok pomarańczowy w puszkach w kształcie walca. Firma A sprzedaje sok w puszkach o promieniu r i wysokości h, a firma B w puszkach o promieniu o 10% większym, a wysokości o 10% mniejszej niż firma A. Ceny puszek soku są takie same. Która firma sprzedaje drożej?
Treść dostępna po opłaceniu abonamentu.Odległość środków okręgów o promieniach 15 cm i 10 cm jest równa 20 cm. Wyznacz odległość środków tych okręgów od punktu przecięcia się prostej przechodzącej przez środki okręgów i wspólnej stycznej do tych okręgów.
Treść dostępna po opłaceniu abonamentu.