Konkurs kuratoryjny z matematyki 2006/2007 – Śląskie – Etap wojewódzki
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP WOJEWÓDZKI – 14 marca 2007 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 12 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj dokładnie treść zadań, zwracając uwagę na to, czy polecenie nakazuje podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- W części I (zadania od 1 do 8) wpisz TAK lub NIE obok każdej z trzech odpowiedzi. Za każdy poprawny wpis otrzymasz 1 punkt – w sumie za każde z tych zadań możesz otrzymać maksymalnie 3 punkty.
- Margines po prawej stronie kartki jest przeznaczony na brudnopis.
- Zabronione jest korzystanie z kalkulatorów i korektorów pisma (ewentualne błędne zapisy należy wyraźnie skreślić).
- Na rozwiązanie wszystkich zadań masz 90 minut.
- Aby zastać laureatem musisz zdobyć co najmniej 36 punktów.
Plik z zadaniami z konkursu kuratoryjnego – etap wojewódzki
Zadania z konkursu kuratoryjnego w pliku pdf.
I część konkursu kuratoryjnego z matematyki – etap wojewódzki
Funkcja y=|m-2|x+3 jest:
Krawędź sześcianu zmniejszono o 50% . Prawdą jest stwierdzenie:
Symbol [x] oznacza największą liczbę całkowitą równą lub mniejszą od x. Prawdą jest, że:
Punkty A=(4,6) i B=(-4,-2) są symetryczne względem punktu S. Punkt S:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Szukamy liczby dwucyfrowej spełniającej warunek: jeżeli pomiędzy jej cyfry wpiszemy 5, to otrzymamy liczbę trzycyfrową 11 razy większą od liczby wyjściowej. Liczba ta:
Wśród 40 uczniów pewnej klasy 17 gra w szachy, 21 umie pływać, a 6 posiada obie te umiejętności. Prawdą jest, że:
Która jest teraz godzina? – pyta Michał ojca. A policz: do końca doby pozostało 3 razy mniej czasu niż upłynęło od jej początku. Teraz jest:
Część II konkursu kuratoryjnego – zadania otwarte
Korzystając z danych przedstawionych na rysunku, wyznacz miary kątów: α, β, γ. Odpowiedź uzasadnij.
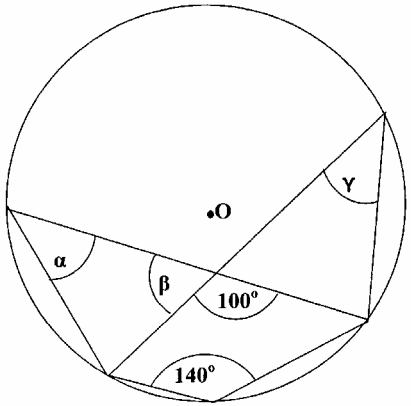Treść dostępna po opłaceniu abonamentu.
Pan Drzewko zakłada plantację choinek. Chce zasadzić choinki tak, aby liczba sadzonek w rzędzie była równa liczbie rzędów. Obliczył, że jeśli obsadzi tyle rzędów, ile zaplanował, to zostaną mu 4 choinki, jeśli zaś doda jeden rząd, to zabraknie mu 25 choinek. Oblicz, ile sadzonek kupił pan Drzewko.
Treść dostępna po opłaceniu abonamentu.Dzieląc pewną liczbę naturalną przez 3, 4, 5, 6, 7 otrzymujemy tę samą resztę równą 2. Wyznacz najmniejszą liczbę o podanej własności większą od 10.
Treść dostępna po opłaceniu abonamentu.Oblicz objętość stożka ściętego, którego powierzchnię boczną (zacieniowaną) przedstawia rysunek.
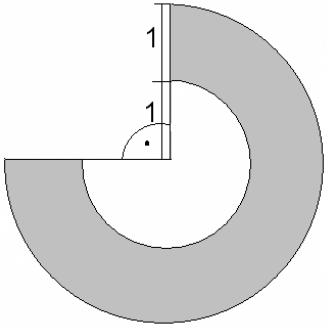Treść dostępna po opłaceniu abonamentu.