Konkurs kuratoryjny z matematyki 2006/2007 – Śląskie – Etap rejonowy
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP REJONOWY – 11 stycznia 2007 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 14 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj dokładnie treść zadań, zwracając uwagę na to, czy polecenie nakazuje podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- W części I (zadania od 1 do 9) wpisz TAK lub NIE obok każdej z trzech odpowiedzi. Za każdy poprawny wpis otrzymasz 1 punkt – w sumie, za każde z tych zadań, możesz otrzymać maksymalnie 3 punkty.
- Margines po prawej stronie kartki jest przeznaczony na brudnopis.
- Zabronione jest korzystanie z kalkulatorów i korektorów pisma (ewentualne błędne zapisy należy wyraźnie skreślić).
- Na rozwiązanie wszystkich zadań masz 90 minut.
- Aby zakwalifikować się do finału musisz zdobyć co najmniej 41 punktów.
Plik z zadaniami z konkursu kuratoryjnego – etap rejonowy
Pobierz zadania z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap rejonowy
Roczna stopa oprocentowania w pewnym banku wynosi 6%, a kapitalizacja odsetek następuje co pół roku. Wpłacono na konto 1000 zł. Po roku bank wypłaci:
Wśród liczb postaci 3n−1, gdzie n jest liczbą całkowitą dodatnią:
Pewien graniastosłup ma 90 krawędzi. Ma on:
Prawdopodobieństwo tego, że losując 3 patyczki spośród 4 o długościach 2cm, 3cm, 4cm i 5cm, zbudujemy trójkąt jest:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Liczba, będąca wartością wyrażenia jest 315+316+317 wielokrotnością liczby:
Liczba dwucyfrowa jest 4 razy większa od sumy swoich cyfr. Prawdą jest, że:
Funkcja liniowa spełnia warunki f(x)=f(x+2)−4 i f(1)=1. Funkcja ta wyraża się wzorem:
Wartość wyrażenia \(\left| 2\sqrt{3}-3\sqrt{2} \right|\) wynosi:
Pojazd przebywa ustaloną drogę ruchem jednostajnym prostoliniowym. Gdy prędkość pojazdu zwiększymy a razy, to czas jazdy:
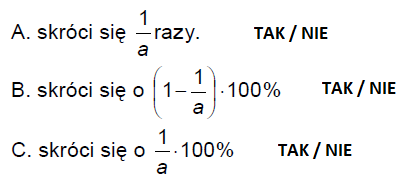Treść dostępna po opłaceniu abonamentu.
Część II konkursu kuratoryjnego z matematyki – zadania otwarte
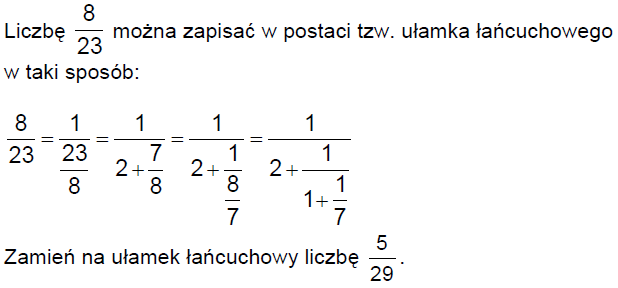Treść dostępna po opłaceniu abonamentu.
Uzupełnij wzór funkcji f(x) i naszkicuj wykres tej funkcji.
Treść dostępna po opłaceniu abonamentu.Wykaż, że liczba \(\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\) jest liczbą naturalną.
Treść dostępna po opłaceniu abonamentu.Przekątna AC prostokąta ABCD jest bokiem podobnego do niego prostokąta ACEF (patrz rys.). Pole wspólnej części tych prostokątów stanowi 40% pola prostokąta ACEF. Znajdź stosunek długości boków prostokąta ABCD.
Treść dostępna po opłaceniu abonamentu.
Trzy szkoły zorganizowały wspólne zawody sportowe. Pierwsza szkoła wystawiła o 25% uczniów więcej niż druga, druga o 4 osoby więcej niż trzecia. Szkoły druga i trzecia wystawiły łącznie o 20 uczniów więcej niż szkoła pierwsza. Oblicz, ilu uczniów z każdej szkoły wzięło udział w zawodach.
Treść dostępna po opłaceniu abonamentu.