Konkurs kuratoryjny z matematyki 2005/2006 – Śląskie – Etap wojewódzki
Konkurs przedmiotowy z matematyki, etap wojewódzki – 15 marca 2006 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 12 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj uważnie treść zadań, zwracając uwagę na to, czy polecenie każe podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- Uwaga! W zadaniach od 1 do 7 wpisz TAK lub NIE obok każdej z trzech odpowiedzi. Za każdy poprawny wpis otrzymasz 1 punkt – w sumie za każde z tych zadań możesz otrzymać maksymalnie 3 punkty.
- Rozwiązania zadań z II części wpisz na oddzielne kartki. Rozwiązania zapisane w brudnopisie nie będą oceniane.
- Na rozwiązanie wszystkich zadań masz 90 minut.
Plik z zadaniami z konkursu kuratoryjnego
Pobierz zadania z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap wojewódzki
Janek zjechał na nartach ze szczytu góry w czasie 4 minut. Trasa narciarska ma 1200 m. Średnia prędkość Janka w trakcie zjazdu wynosiła:
Wśród 10 kolejnych liczb naturalnych liczb podzielnych przez 3 może być:
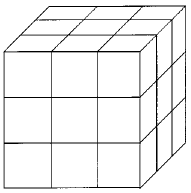
Kostkę sześcienną pomalowaną na zielono rozcięto tak, jak pokazano na rysunku i otrzymane kostki przemieszano. Następnie wylosowano 1 kostkę. Prawdą jest, że:
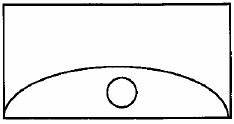
Do naczynia w kształcie odwróconego stożka wlano płyn do 3/4 wysokości naczynia. Płyn zajmuje:
Figurę pokazaną na rysunku należy pokolorować tak, aby sąsiadujące obszary miały różne kolory. Mając 3 różne kolory można to zrobić na:
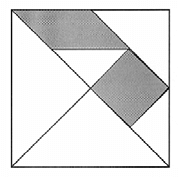
Tangram (na rysunku obok) powstał z kwadratu o boku 1. Dwa zamalowane czworokąty:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
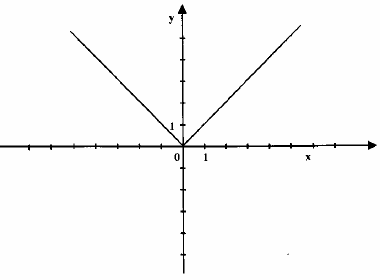
Rysunek przedstawia wykres funkcji:
II część konkursu kuratoryjnego z matematyki – etap wojewódzki
Uzasadnij, że dla n naturalnego każda liczba postaci 2n+2n+1+2n+2+2n+3 jest podzielna przez 5.
Treść dostępna po opłaceniu abonamentu.Do puszki w kształcie walca o średnicy dna wynoszącej 20 cm wrzucono metalową kulkę. Poziom wody w puszce podniósł się o 3 cm. Oblicz, jaką długość ma promień wrzuconej kulki.
Treść dostępna po opłaceniu abonamentu.Z kwadratu wycięto ośmiokąt o boku 1 jak pokazano na rysunku.Oblicz pole tego ośmiokąta.
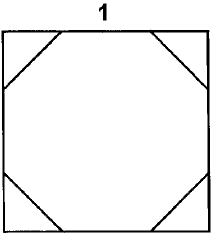Treść dostępna po opłaceniu abonamentu.
Z relacji kierowcy wynika, że na trasie 400 km jego samochód zużył 32,5 l benzyny. Samochód ten zużywając 1 litr paliwa, może przejechać 10 km w mieście lub 12,5 km na autostradzie. Oblicz, ile kilometrów przejechał kierowca w mieście, a ile na autostradzie.
Treść dostępna po opłaceniu abonamentu.W trójkącie ABC przez środek środkowej CC’ poprowadzono prostą równoległą do boku BC. Prosta ta przecina bok AC w punkcie D. Sporządź odpowiedni rysunek. Wyznacz wartość \(\frac{DC}{DA}\).
Treść dostępna po opłaceniu abonamentu.