Konkurs kuratoryjny z matematyki 2005/2006 – Śląskie – Etap rejonowy
Konkurs przedmiotowy z matematyki, etap rejonowy – 11 stycznia 2006 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 14 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj uważnie treść zadań, zwracając uwagę na to, czy polecenie każe podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- Uwaga! W zadaniach od 1 do 8 wpisz TAK lub NIE obok każdej z trzech odpowiedzi.
- Za każdy poprawny wpis otrzymasz 1 punkt – w sumie za każde z tych zadań możesz otrzymać maksymalnie 3 punkty.
- Na rozwiązanie wszystkich zadań masz 90 minut.
Plik z zadaniami konkursu kuratoryjnego
Pobierz zadania z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap rejonowy
Liczbą niewymierną może być:
Funkcja liniowa spełniająca warunki: f(x)= f(x+1)−3 i f(1)=2 ma postać:
Jeżeli w trójkącie równoramiennym kąt przy jednym z wierzchołków ma miarę 26 stopni, to kąt przy jednym z pozostałych wierzchołków może mieć miarę:
Plan w skali 1:2 500 przedstawia ogród w kształcie trójkąta prostokątnego o przyprostokątnych 3 cm i 4 cm. O rzeczywistym ogrodzie można powiedzieć, że:
1 mol to taka ilość materii, która zawiera 6⋅1023 odpowiednio atomów, cząsteczek lub jonów. W 0,25 mola wody zawartych jest:
Miara kąta wpisanego opartego na 1/10 okręgu wynosi:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Na szczyt góry prowadzi 5 dróg. Turysta pokonuje trasę na szczyt i z powrotem. Może to uczynić maksymalnie na:
Z kartonu o wymiarach 30 cm na 21 cm można na pewno wyciąć w całości, bez sklejania:
II część konkursu kuratoryjnego z matematyki – etap rejonowy
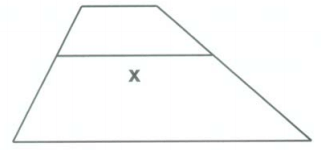
W trapezie o podstawach długości 9 cm i 16 cm połączono ramiona odcinkiem o długości x równoległym do podstaw tak, że otrzymano dwa trapezy podobne. Wyznacz długość odcinka x i podaj skalę podobieństwa tych trapezów.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Funkcja f(n) każdej liczbie naturalnej n przyporządkowuje resztę powstałą z dzielenia liczby n przez liczbę 5. Określ zbiór wartości tej funkcji oraz narysuj wykres tej funkcji dla n<20. Uwaga: zero zaliczamy do zbioru liczb naturalnych.
Treść dostępna po opłaceniu abonamentu.Uczniów biorących udział w olimpiadzie matematycznej należało umieścić w salach tak, by w każdej sali była ta sama liczba osób, przy czym nie więcej niż 32 osoby w jednej sali. Kiedy najpierw w każdej sali umieszczono po 22 osoby, dla jednego zawodnika zabrakło miejsca. Gdy zaś z jednej sali zrezygnowano, miejsc w pozostałych wystarczyło dla wszystkich. Oblicz, ilu zawodników wzięło udział w olimpiadzie oraz ile sal przygotowano dla nich początkowo.
Treść dostępna po opłaceniu abonamentu.Droga krajowa o szerokości 6 m przecina pod kątem 45° drogę lokalną, która ma szerokość równą 4 m. Oblicz powierzchnię części wspólnej obu dróg. Sporządź odpowiedni rysunek.
Treść dostępna po opłaceniu abonamentu.W układzie współrzędnych XOY zaznacz zbiór wszystkich punktów, których współrzędne spełniają jednocześnie warunki: |y|≤2 i y≥|x|−4 gdzie x, y są liczbami rzeczywistymi. Oblicz pole zaznaczonej figury odczytując dane z rysunku.
Treść dostępna po opłaceniu abonamentu.Kamil i Tomek wyszli jednocześnie z tego samego domu do szkoły. Długość kroku Kamila jest o 20% mniejsza od długości kroku Tomka. Który z chłopaków wcześniej dotrze do szkoły tą samą drogą, jeżeli wiadomo, że Kamil robi w tym samym czasie o 20% kroków więcej niż Tomek? Odpowiedź uzasadnij. Przyjmujemy, że każdy z chłopców porusza się jednostajnie.
Treść dostępna po opłaceniu abonamentu.



