Konkurs kuratoryjny z matematyki 2003/2004 – Śląskie – Etap wojewódzki

Jaką cyfrę jedności ma wynik działania 23 ⋅ 79 ⋅ 58 ?

Które z poniższych określeń liczby 0,(5) jest prawdziwe?

Ile jest liczb całkowitych dodatnich wśród rozwiązań nierówności \(1-\sqrt{2}\le 2+x\)?

Ile z poniższych stwierdzeń jest prawdziwych?
a) 50% liczby 80 jest równe 80% liczby 50.
b) 3/4 liczby 72 jest równe 54.
c) 2/91 jest większe od 2/93.
d) 3,106 : 1,6 jest większe 2

Jeśli „x” dzielone przez „y” równa się 4/5, a „y” dzielone przez „z” równa się 3/10, to ile to jest „x” dzielone przez „z”?

Pociąg o długości 100m jadący z prędkością 90km/h wjeżdża do tunelu o długości 300m. Ile potrzeba czasu, aby cały pociąg przejechał przez tunel?

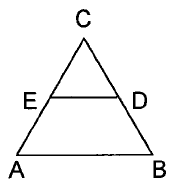
Trójkąt równoboczny ABC ma pole 40. Punkty D i E są środkami jego boków. Ile wynosi pole trapezu ABDE?

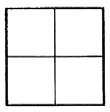
Kwadrat na rysunku podzielony został na cztery mniejsze kwadraty. Jeżeli obwód dużego kwadratu wynosi 1, to jaką długość ma obwód małego kwadratu?

Z masy marcepanowej w kształcie kuli o promieniu10 cm cukiernik chce zrobić cukierki w kształcie kuli o promieniu 1 cm. Ile cukierków może wykonać cukiernik z posiadanej masy?

Jaką figurę utworzy zaznaczona na siatce linia po złożeniu tej siatki (rysunek obok)?

Rozstrzygnij, czy liczba \(\underbrace{11…1}_{14}\underbrace{22…2}_{7}\underbrace{11…1}_{14}+6\) jest pierwsza czy złożona? Odpowiedź uzasadnij.

Co jest większe: pole koła opisanego na trójkącie prostokątnym, czy suma pól półkoli zbudowanych na jego wszystkich bokach jako na średnicach? Odpowiedź uzasadnij.

Zapisz w najprostszej postaci wyrażenie \(\left| 6+x \right|+\left( \frac{\left| x-2 \right|}{x-2}-2 \right)-\left| 1-x \right|\) dla 3<x<5.

Suma kątów wewnętrznych wielokąta wypukłego jest funkcją liczby jego boków. Podaj i uzasadnij wzór tej funkcji, a następnie wykonaj jej wykres dla wielokątów o liczbie boków mniejszej od 10.