Konkurs kuratoryjny z matematyki 2003/04 – Śląskie – Etap szkolny
Konkurs przedmiotowy z matematyki, etap szkolny – 19 listopada 2003 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 11 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj uważnie treść zadań, zwracając uwagę na to, czy polecenie każe podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie lub w inny sposób uzasadnić wynik).
- Na rozwiązanie wszystkich zadań masz 90 minut.
Plik z zadaniami z konkursu kuratoryjnego – etap szkolny 2003/2004
Tutaj możesz pobrać plik z zadaniami.
Zadania z konkursu kuratoryjnego
Zapisz liczbę 20 za pomocą pięciu dwójek i znanych działań.
Na poniższej osi liczbowej zaznaczono punkty A i B. Podaj współrzędną punktu D takiego, aby odcinek AD miał długość \(1\frac{1}{12}\) jednostki, a odcinek BD długość \(\frac{3}{4}\) jednostki.

Oblicz, o ile procent zmniejszy się pole koła, jeżeli długość jego promienia zmniejszymy o 20%.
Podziel dowolny trapez na dwie części tak, aby można było z tych części złożyć trójkąt. Uzasadnij poprawność podziału.
Znajdź liczby a i b takie, aby spełniona była równość \({{\left( a+b \right)}^{2}}=19+6\sqrt{2}\)
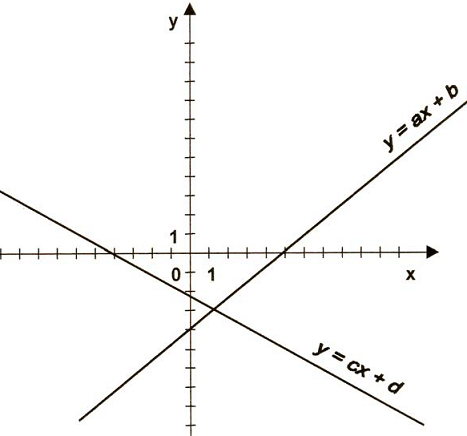
Na rysunku poniżej przedstawiono wykresy funkcji: y=ax+b, y=cx+d. Określ i uzasadnij, jaki jest znak liczb a, b, c, d oraz iloczynu abcd.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Podaj i uzasadnij, który ze znaków <, >, = należy wpisać pomiędzy liczby 3260…6450
Treść dostępna po opłaceniu abonamentu.Trójkąt równoboczny i sześciokąt foremny mają równe obwody. Oblicz, jaki jest stosunek pola trójkąta do pola sześciokąta.
Treść dostępna po opłaceniu abonamentu.Stosunek dwóch liczb jest równy 3:4, a suma ich kwadratów równa się 100. Znajdź te liczby. Podaj wszystkie rozwiązania.
Treść dostępna po opłaceniu abonamentu.Antek i Bartek zobaczyli na wystawie księgarni album o żaglowcach, którego cena w złotych wyrażała się liczbą pierwszą. Nie mógł go kupić Antek, bo mu brakowało 74 zł, nie mógł go kupić Bartek, bo mu brakowało 9 zł, nie mogli go kupić obaj za wspólne pieniądze, bo mieli ich za mało. Oblicz, ile złotych kosztował album.
Treść dostępna po opłaceniu abonamentu.Wykaż, że istnieje tylko jeden trójkąt prostokątny o bokach, których długości są kolejnymi liczbami naturalnymi.
Treść dostępna po opłaceniu abonamentu.



