Konkurs kuratoryjny z matematyki 2002/2003 – Śląskie – Etap wojewódzki
Konkurs przedmiotowy z matematyki. Finał wojewódzki – 4 kwietnia 2003 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z dwóch części. Pierwsza zawiera 10 zadań zamkniętych, druga 4 zadania rozszerzonej odpowiedzi. Przy numerze zdania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj uważnie treść zadań. Odpowiedzi do zadań w części I zaznacz w tabeli. Pozostałe rozwiązania wpisz na oddzielne kartki.
- Na rozwiązanie wszystkich zadań masz 90 minut.
Pliki z zadaniammi z konkursu kuratoryjnego
Zadania konkursowymi do pobrania znajdziesz tutaj.
I część konkursu kuratoryjnego z matematyki.
Ile wynosi polowa liczby 424?
Dane są liczby:\(a=\sqrt{2},\,\,b=-\sqrt{2}+0,5\sqrt{8},\,\,c=\sqrt{2}+0,5\sqrt{8},\,\,d=3,\left( 1 \right).\) Które z tych liczb są wymierne?
Ile wynosi wartość wyrażenia 5572 – 4432?
Kilogram bananów przed obniżką kosztował x zł, a po obniżce y zł. O ile procent obniżono cenę kilograma bananów?
Ile wynosi wartość wyrażenia \(\left( x-1 \right)\cdot \left( x-2 \right)\cdot …\cdot \left( x-99 \right)\cdot \left( x-100 \right),\,\,dla\,\,x=13\,\,?\)
Na kwadratowej działce o powierzchni jednego ara założono klomb w kształcie kwadratu w ten sposób, że połączono środki kolejnych boków. Ile m2 zajmuje ten klomb?
Trójkąt równoboczny o boku c ma pole powierzchni S. Jakie jest pole trójkąta o boku \(c\sqrt{3}\)?
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Sześcian przecięto płaszczyzną przechodzącą przez przekątną sześcianu i środek jednej krawędzi bocznych. Jaki kształt ma tak otrzymany przekrój?
Dane są proste o równaniach \(y=\frac{1}{4}x-1\,\,\,\,i\,\,\,\,y=-\frac{1}{4}x-1.\)Które zdanie jest prawdziwe?
Jaką długość ma odcinek x (patrz rysunek)?
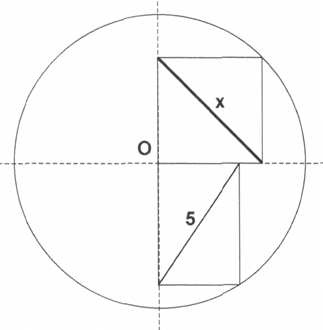
II część konkursu kuratoryjnego z matematyki. Zadania za 4 i 5 punktów
Dana jest liczba rzeczywista a. Wyznacz wszystkie liczby x spełniające równanie:
x2 – a2 + x – a = 0
Uczniowie napisali pracę kontrolną. 30% uczniów otrzymało ocenę bardzo dobrą, 40% otrzymało ocenę dobrą, 8 uczniów dostateczną, pozostali dopuszczającą. Średnia ocen wyniosła 3,9. Oblicz, ilu uczniów pisało pracę kontrolną.
Treść dostępna po opłaceniu abonamentu.Dany jest wielokąt złożony z punktów, których współrzędne spełniają warunki: −1≤x≤3 i 0≤y≤2. Wyznacz wartości b, dla których prosta o równaniu y=-x+b ma dokładnie jeden punkt wspólny z tym wielokątem. Wykonaj rysunek.
Treść dostępna po opłaceniu abonamentu.Dany jest kąt ostry o wierzchołku A. Na jednym ramieniu tego kąta zaznacz punkt B, na drugim ramieniu punkt C tak, |AC|>|AB|. Na ramieniu AC wyznacz konstrukcyjnie punkt D tak, aby |AD|+|DB|=|AC|. Przeprowadź analizę zadania, wykonaj konstrukcję, opisz ją i podaj uzasadnienie (dowód poprawności).
Treść dostępna po opłaceniu abonamentu.



