Podstawowa matura z matematyki – Maj 2020 CKE
Wartość wyrażenia \({{x}^{2}}-6x+9\quad dla\quad x=\sqrt{3}+3\) jest równa
Liczba \(\frac{{{2}^{50}}\cdot {{3}^{40}}}{{{36}^{10}}}\) jest równa
Liczba \({{\log }_{5}}\sqrt{125}\) jest równa
Cenę x pewnego towaru obniżono o 20% i otrzymano cenę y. Aby przywrócić cenę x, nową cenę y należy podnieść o
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Zbiorem wszystkich rozwiązań nierówności \(3\left( 1-x \right)>2\left( 3x-1 \right)-12x\) jest przedział
Suma wszystkich rozwiązań równania \(x\left( x-3 \right)\left( x+2 \right)=0\) jest równa
Funkcja kwadratowa f jest określona wzorem \(f\left( x \right)=a\left( x-1 \right)\left( x-3 \right).\) Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt W = (2,1) .
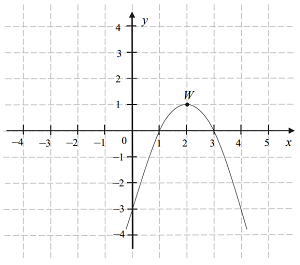
Współczynnik a we wzorze funkcji f jest równy
Największa wartość funkcji f w przedziale \(\left\langle 1,4 \right\rangle \) jest równa
Osią symetrii paraboli będącej wykresem funkcji f jest prosta o równaniu
Równanie \(x\left( x-2 \right)={{\left( x-2 \right)}^{2}}\) w zbiorze liczb rzeczywistych
Na rysunku przedstawiono fragment wykresu funkcji liniowej f określonej wzorem
f (x)= ax+b.
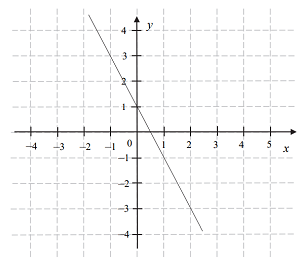
Współczynniki a oraz b we wzorze funkcji f spełniają zależność
Funkcja f jest określona wzorem \(f\left( x \right)={{4}^{-x}}+1\) dla każdej liczby rzeczywistej x.
Liczba \(f\left( \frac{1}{2} \right)\) jest równa
Proste o równaniach \(y=\left( m-2 \right)x\quad oraz\quad y=\frac{3}{4}x+7\) są równoległe. Wtedy
Ciąg \(\left( {{a}_{n}} \right)\) jest określony wzorem \({{a}_{n}}=2{{n}^{2}}\ dla\ n\ge 1.\) Różnica \({{a}_{5}}-{{a}_{4}}\) jest równa
W ciągu arytmetycznym \(\left( {{a}_{n}} \right)\), określonym dla \(n\ge 1,\) czwarty wyraz jest równy 3, a różnica tego ciągu jest równa 5. Suma \({{a}_{1}}+{{a}_{2}}+{{a}_{3}}+{{a}_{4}}\) jest równa
Punkt \(A=\left( \frac{1}{3},-1 \right)\) należy do wykresu funkcji liniowej f określonej wzorem \(f\left( x \right)=3x+b\). Wynika stąd, że
Punkty A, B, C, D, leżą na okręgu o środku w punkcie O. Kąt środkowy DOC ma miarę 118° (zobacz rysunek).
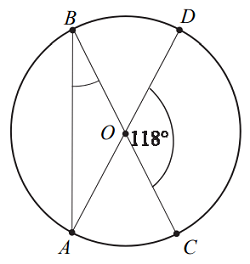
Miara kąta ABC jest równa
Prosta przechodząca przez punkty A = (3,-2) i B = (-1,6) jest określona równaniem
Dany jest trójkąt prostokątny o kątach ostrych \(\alpha \ i\ \beta \) (zobacz rysunek).
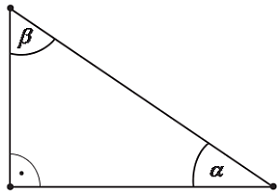
Wyrażenie \(2\cos \alpha -\sin \beta \) jest równe
Punkt B jest obrazem punktu A = (−3, 5) w symetrii względem początku układu współrzędnych. Długość odcinka AB jest równa
Ile jest wszystkich dwucyfrowych liczb naturalnych utworzonych z cyfr: 1, 3, 5, 7, 9, w których cyfry się nie powtarzają?
Pole prostokąta ABCD jest równe 90. Na bokach AB i CD wybrano – odpowiednio – punkty P i R, takie, że \(\frac{\left| AP \right|}{\left| PB \right|}=\frac{\left| CR \right|}{\left| RD \right|}=\frac{3}{2}\) (zobacz rysunek).
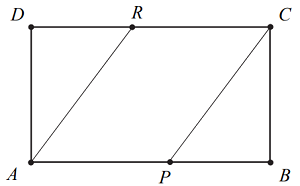
Pole czworokąta APCR jest równe:
Cztery liczby: 2, 3, a, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
Przekątna sześcianu ma długość \(4\sqrt{3}.\) Pole powierzchni tego sześcianu jest równe
Rozwiąż nierówność \(2\left( x-1 \right)\left( x+3 \right)>x-1.\)
Treść dostępna po opłaceniu abonamentu.Rozwiąż równanie \(\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}-2x \right)=0.\)
Treść dostępna po opłaceniu abonamentu.Wykaż, że dla każdych dwóch różnych liczb rzeczywistych a i b prawdziwa jest nierówność
Trójkąt ABC jest równoboczny. Punkt E leży na wysokości CD tego trójkąta oraz \(\left| CE \right|=\frac{3}{4}\left| CD \right|.\) Punkt F leży na boku BC i odcinek EF jest prostopadły do BC (zobacz rysunek).
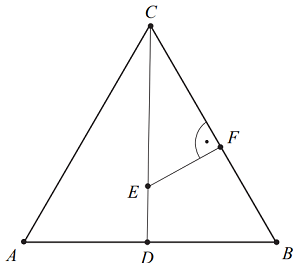
Wykaż, że \(\left| CF \right|=\frac{9}{16}\left| CB \right|.\)
Treść dostępna po opłaceniu abonamentu.Rzucamy dwa razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że co najmniej jeden raz wypadnie ścianka z pięcioma oczkami.
Treść dostępna po opłaceniu abonamentu.Kąt \(\alpha\) jest ostry i spełnia warunek \(\frac{2\sin \alpha +3\cos \alpha }{\cos \alpha }=4.\) Oblicz tangens kąta \(\alpha\).
Treść dostępna po opłaceniu abonamentu.Dany jest kwadrat ABCD, w którym \(A=\left( 5,-\frac{5}{3} \right).\) Przekątna BD tego kwadratu jest zawarta w prostej o równaniu \(y=\frac{4}{3}x.\) Oblicz współrzędne punktu przecięcia przekątnych AC i BD oraz pole kwadratu ABCD.
Treść dostępna po opłaceniu abonamentu.Wszystkie wyrazy ciągu geometrycznego \(\left( {{a}_{n}} \right),\) określonego dla n ≥ 1, są dodatnie. Wyrazy tego ciągu spełniają warunek \(6{{a}_{1}}-5{{a}_{2}}+{{a}_{3}}=0.\) Oblicz iloraz q tego ciągu należący do przedziału \(\left\langle 2\sqrt{2},\ 3\sqrt{2} \right\rangle .\)
Treść dostępna po opłaceniu abonamentu.Dany jest ostrosłup prawidłowy czworokątny ABCDS, którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy \(\sqrt{7}.\) Oblicz objętość tego ostrosłupa.
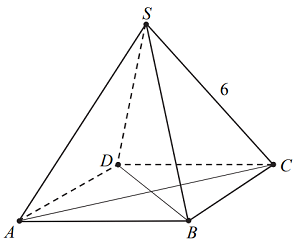 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.




