Trójkąt 30 60 90 i Trójkąt 45 45 90 – Testy ósmoklasisty
Trójkąt 30 60 90
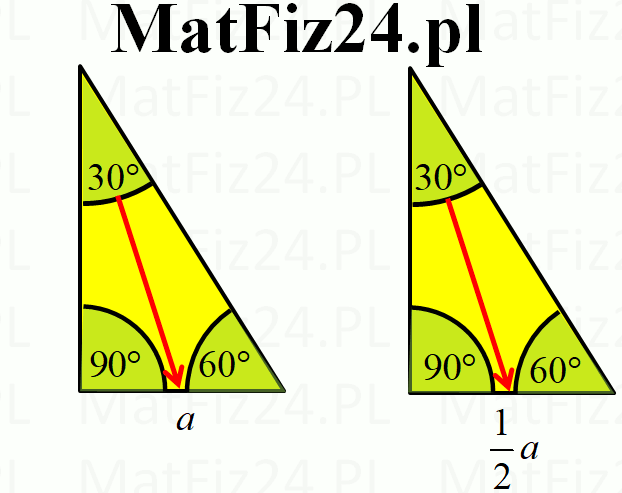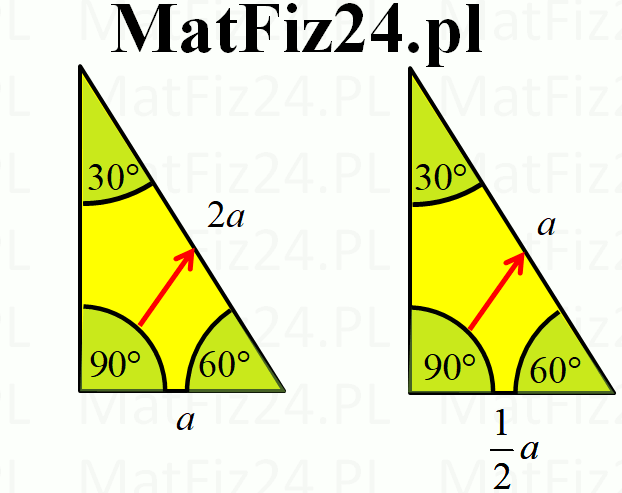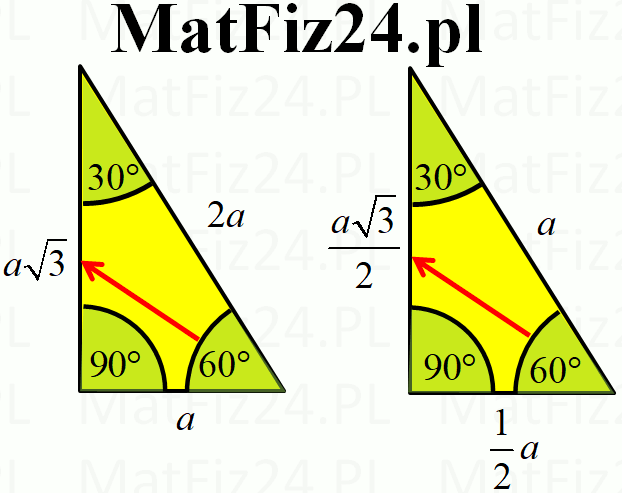
Trójkąt 30°,60°,90° to połowa trójkąta równobocznego. Na przeciw kąta 30° jest najkrótszy bok oznaczony przez symbol a, na przeciw 90° jest najdłuższy bok oznaczony przez 2a, a na przeciw 60° jest średni bok oznaczony przez \(a\sqrt{3}\). Zatem w skrócie możemy powiedzieć, że boki są w stosunku: \(a,2a,a\sqrt{3}\).
W książkach są dwa alternatywne oznaczenia boków trójkąta 30°,60°,90°. Zobacz rysunek niżej. W zadaniach jednak łatwiej stosuje się pierwsze oznaczenia wyrażony symbolami: \(a,2a,a\sqrt{3}\).
Trójkąt 45 45 90
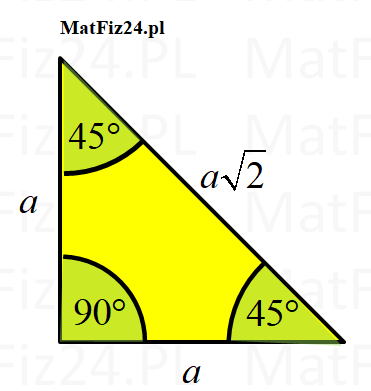
Trójkąt 45°,45°,90° to połowa kwadratu. Na przeciw ka zdego kąta 45° jest przyprostokątna oznaczona przez symbol a, na przeciw 90° jest najdłuższy bok, przeciwprostokątna oznaczony przez 2a, a na przeciw 60° jest średni bok oznaczony przez \(a\sqrt{2}\). Zatem w skrócie możemy powiedzieć, że boki są w stosunku: \(a,a,a\sqrt{2}\).
Zobacz na rysunku jak prezentują się wzory na trójkącie 45°,45°,90°.
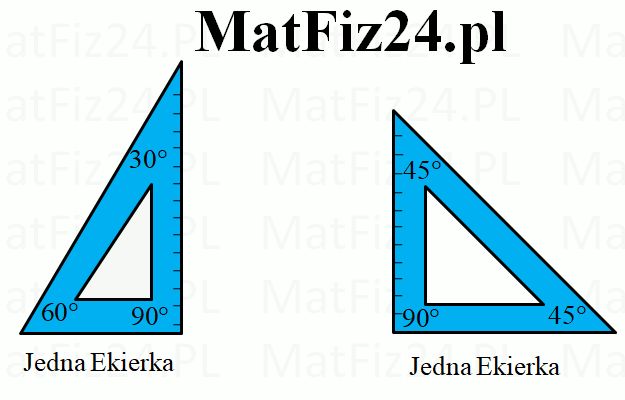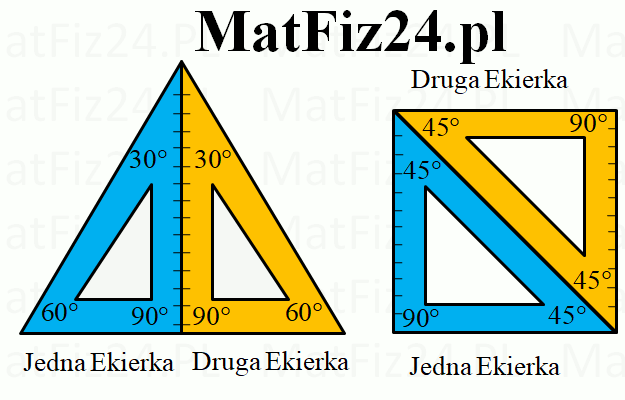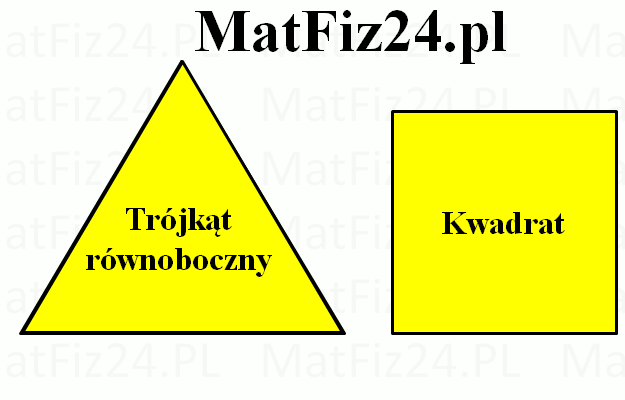
Trójkąty 30°,60°,90° i 45°,45°,90° jako trójkąty ekierkowe
Trójkąt 30°,60°,90° ma kształt ekierki, która jest połową trójkąta równobocznego. Zatem dwie takie ekierki tworzą trójkąt równoboczny.
Trójkąt 45°,45°,90° ma kształt ekierki, która jest połową kwadratu. Zatem dwie takie ekierki tworzą kwadrat. Zobacz animację niżej.
Trójkąty o kątach 30°,60°,90° i 45°,45°,90° – Zadania
Na przekątnej BD kwadratu ABCD o boku długości 4 zbudowano trójkąt równoboczny BED.
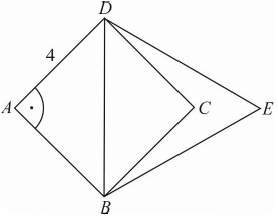
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta BED jest równe
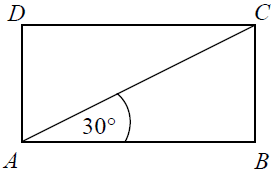
Przekątna prostokąta ABCD nachylona jest do jednego z jego boków pod kątem 30°. Uzasadnij, że pole prostokąta ABCD jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
Kąt ostry rombu ma miarę 45º, a wysokość rombu jest równa h.
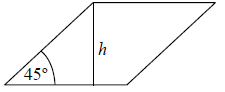
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pole tego rombu można wyrazić wzorem
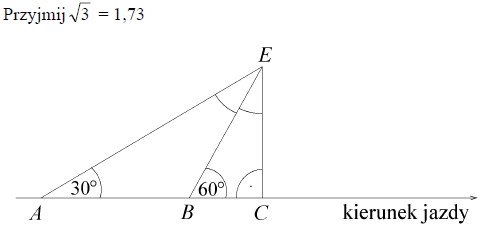
Jadąc długą, prostą drogą, Ewa widziała elektrownię wiatrową zaznaczoną na rysunku literą E. Z punktu A widać było elektrownię pod kątem 30º od kierunku jazdy, a z punktu B – pod kątem 60º. Długość odcinka AB jest równa 20 km. Po pewnym czasie, przejeżdżając przez punkt C, Ewa minęła elektrownię.
Wpisz na rysunku miary kątów zaznaczonych łukami (∡ BEC i ∡ AEB). Oblicz odległość (BE) elektrowni od punktu B oraz odległość (CE) elektrowni od drogi. Zapisz obliczenia. Wynik zaokrąglij do części dziesiątych.