Testy ósmoklasisty – wybrane zadania z egzaminu gim. 2013
Informacje do zadania 2.
W tabeli przedstawiono informacje dotyczące wieku wszystkich uczestników obozu narciarskiego.
Na którym diagramie poprawnie przedstawiono procentowy podział uczestników obozuze względu na wiek? Wybierz odpowiedź spośród podanych.
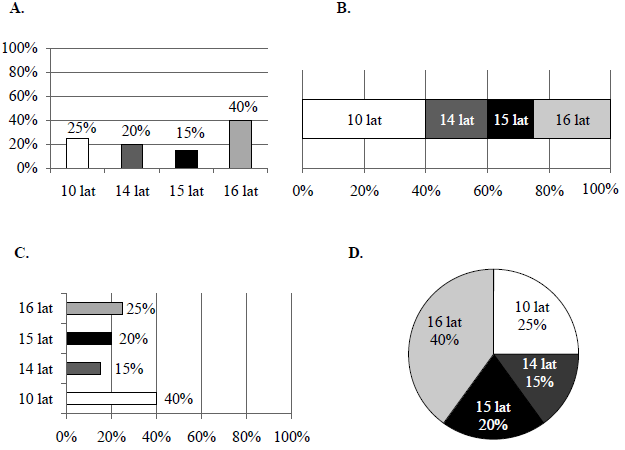
W pewnej hurtowni za 120 jednakowych paczek herbaty trzeba zapłacić 1500 zł.
Ile takich paczek herbaty można kupić w tej hurtowni za 600 zł, przy tej samej cenie za jedną paczkę? Wybierz odpowiedź spośród podanych.
A. 48 B. 50 C. 52 D. 56
Cena brutto = cena netto + podatek VAT
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Wybierz odpowiedź spośród podanych.
A. Jedna liczba. B. Dwie liczby. C. Trzy liczby. D. Cztery liczby.
Treść dostępna po opłaceniu abonamentu.Dane są liczby: a = (–2)12, b = (–2)11, c = 210.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczby te uporządkowane od najmniejszej do największej to:
A. c, b, a. B. a, b, c. C. c, a, b. D. b, c, a.
Treść dostępna po opłaceniu abonamentu.Dane są liczby x i y spełniające warunki: x < 0 i y < x.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
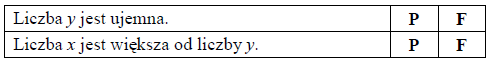 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Informacje do zadań 8. i 9.
Wykres przedstawia zależność ilości farby pozostałej w pojemniku (w litrach) od powierzchni ściany (w m2) pomalowanej farbą z tego pojemnika.
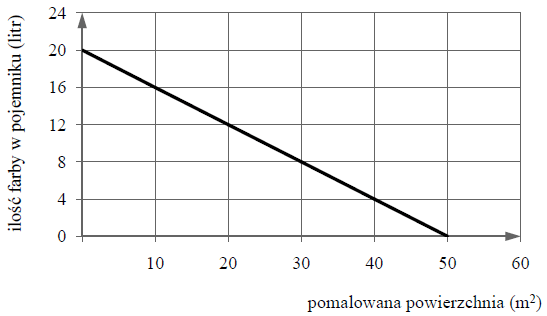
Ile farby pozostało w pojemniku po pomalowaniu 30 m2 ściany? Wybierz odpowiedźspośród podanych.
A. 8 litrów B. 12 litrów C. 16 litrów D. 20 litrów
Treść dostępna po opłaceniu abonamentu.Ile farby zużyto na pomalowanie 10 m2 ściany? Wybierz odpowiedź spośród podanych.
A. 4 litry B. 8 litrów C. 10 litrów D. 16 litrów
Treść dostępna po opłaceniu abonamentu.W pudełku było 20 kul białych i 10 czarnych. Dołożono jeszcze 10 kul białych i 15 czarnych.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Średnia prędkość samochodu na trasie przebytej w czasie 4 godzin wyniosła 60km/h.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
W prostopadłościennym akwarium, o wymiarach podanych na rysunku, woda sięga 2/3 jego wysokości.
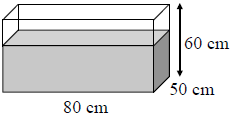
Ile litrów wody jest w akwarium? Wybierz odpowiedź spośród podanych.
A. 16000 litrów B. 1600 litrów C. 160 litrów D. 16 litrów
Treść dostępna po opłaceniu abonamentu.W równoległoboku ABCD bok AB jest dwa razy dłuższy od boku AD. Punkt K jest środkiem boku AB, a punkt L jest środkiem boku CD.
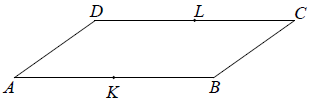
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
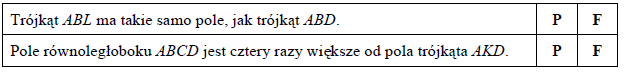 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Jeden z kątów wewnętrznych trójkąta ma miarę α, drugi ma miarę o 30° większą niż kąt α, a trzeci ma miarę trzy razy większą niż kąt α.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Trójkąt ten jest
A. równoboczny.
B. równoramienny.
C. rozwartokątny.
D. prostokątny.
Na rysunkach I–IV przedstawiono cztery pary trójkątów.
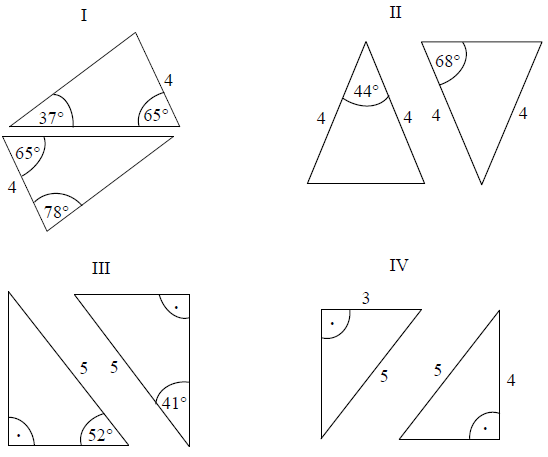
Na którym rysunku trójkąty nie są przystające? Wybierz odpowiedź spośród podanych.
A. I B. II C. III D. IV
Treść dostępna po opłaceniu abonamentu.Kąt ostry rombu ma miarę 45º, a wysokość rombu jest równa h.
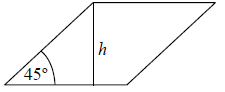
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pole tego rombu można wyrazić wzorem
Siatka ostrosłupa składa się z kwadratu i trójkątów równobocznych zbudowanych na bokach tego kwadratu.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
W pewnej klasie liczba chłopców stanowi 80% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze trzech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
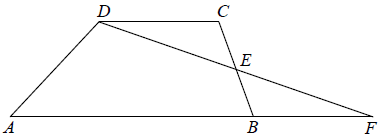
Treść dostępna po opłaceniu abonamentu.Na rysunku przedstawiono trapez ABCD i trójkąt AFD. Punkt E leży w połowie odcinka BC. Uzasadnij, że pole trapezu ABCD i pole trójkąta AFD są równe.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe 80 cm2, a pole jego powierzchni całkowitej wynosi 144 cm2. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.



