Testy ósmoklasisty – wybrane zadania z egzaminu gim. 2012
Na diagramie przedstawiono wyniki pracy klasowej z matematyki w pewnej klasie.
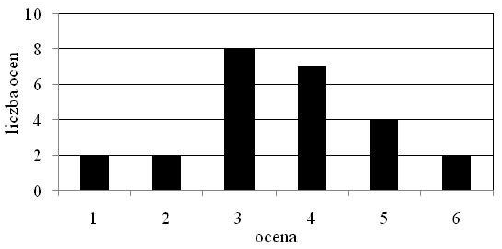
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że
A. pracę klasową pisało 30 uczniów.
B. najczęściej powtarzającą się oceną jest 4.
C. mediana wyników z pracy klasowej wynosi 2.
D. średnia wyników z pracy klasowej jest równa 3,6.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
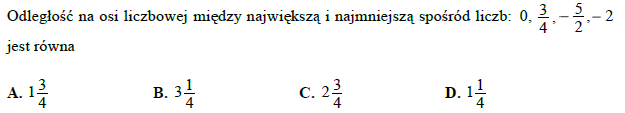
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Połowa uczestników wycieczki urodziła się w Polsce, co trzeci urodził się w Niemczech, a pięciu pozostałych we Francji. W wycieczce brało udział
A. 26 osób. B. 30 osób. C. 46 osób. D. 60 osób.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Treść dostępna po opłaceniu abonamentu.
Glazurnik układał płytki. Wykres przedstawia liczbę ułożonych płytek w zależności od czasu w trakcie ośmiogodzinnego dnia pracy.
Na podstawie wykresu wybierz zdanie fałszywe.
A. O godzinie 1000 glazurnik rozpoczął godzinną przerwę.
B. Od 700 do 800 glazurnik ułożył mniej płytek niż od 1100 do 1200.
C. W ciągu każdej godziny glazurnik układał taką samą liczbę płytek.
D. Przez ostatnie trzy godziny pracy glazurnik ułożył 50 płytek.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Cena płyty kompaktowej po 30% obniżce wynosi 49 zł. Cena tej płyty przed obniżką była równa
A. 14,70 zł. B. 34,30 zł. C. 63,70 zł. D. 70,00 zł.
Treść dostępna po opłaceniu abonamentu.Informacje do zadań 8. i 9.
W turnieju szachowym wzięło udział 48 uczniów pewnego gimnazjum. Liczby uczestników turnieju z klas pierwszych, drugich i trzecich są do siebie w proporcji 3 : 8 : 5.
Jaki procent uczestników turnieju stanowili drugoklasiści? Wybierz odpowiedź spośród podanych.
A. 17% B. 24% C. 33% D. 50%
Treść dostępna po opłaceniu abonamentu.Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba uczniów klas pierwszych, którzy wzięli udział w turnieju, jest równa
A. 8 B. 9 C. 10 D. 11
Treść dostępna po opłaceniu abonamentu.Organizatorzy konkursu matematycznego przygotowali zestaw, w którym było 10 pytań z algebry i 8 pytań z geometrii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z algebry.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Treść dostępna po opłaceniu abonamentu.
Informacje do zadań 11.–13.
Małgosia narysowała równoległobok położony w układzie współrzędnych tak jak na pierw-szym rysunku. Kolejne przystające do niego równoległoboki rysowała w taki sposób, że dol-ny lewy wierzchołek rysowanego równoległoboku był środkiem górnego boku poprzedniego równoległoboku (rysunek 2.).
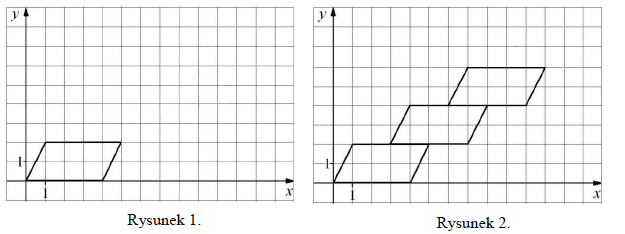
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Małgosia narysowała w opisany sposób czwarty równoległobok. Współrzędna y prawego górnego wierzchołka tego równoległoboku jest równa
A. 8 B. 9 C. 10 D. 11
Treść dostępna po opłaceniu abonamentu.Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Agnieszka narysowała w taki sam sposób n równoległoboków. Współrzędna y prawego gór-nego wierzchołka ostatniego równoległoboku jest równa
A. n + 2 B. 2n C. 2n + 2 D. 4n
Treść dostępna po opłaceniu abonamentu.Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Współrzędne prawego górnego wierzchołka ostatniego narysowanego równoległoboku są równe (a,b). Współrzędne takiego wierzchołka w następnym równoległoboku będą równe
A. (a + 4,b + 2) B. (a + 2,b + 3) C. (a + 3,b + 2) D. (a + 3,b + 1)
Treść dostępna po opłaceniu abonamentu.Piechur porusza się z prędkością 4km/h . Każdy jego krok ma długość 0,8 m.
Ile kroków wykona piechur w czasie 12 minut? Wybierz odpowiedź spośród podanych.
A. 1000 kroków
B. 800 kroków
C. 640 kroków
D. 100 kroków
W prostokątnym układzie współrzędnych umieszczone są dwa przystające trójkąty oraz prosta p tak, jak na rysunku.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeden trójkąt jest symetryczny do drugiego względem
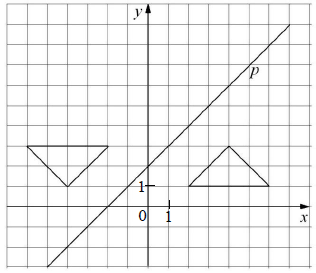
A. osi y.
B. prostej p.
C. punktu (1,3).
D. punktu przecięcia prostej p i osi y.
E. początku układu współrzędnych.
Kształt i wymiary deski do krojenia przedstawiono na rysunku.
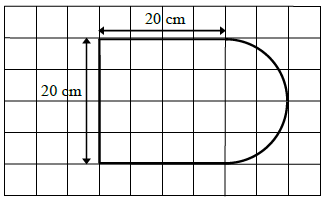
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Powierzchnia tej deski (w cm2) jest równa
A. 400 + 50Π
B. 40 + 50Π
C. 400 + 100Π
D. 40 + 100Π
Basen ma kształt prostopadłościanu, którego podstawa (dno basenu) ma wymiary 15 m x 10 m. Do basenu wlano 240 m3 wody, która wypełniła go do 4/5 głębokości.
Jaka jest głębokość tego basenu? Wybierz odpowiedź spośród podanych.
A. 1,28 m B. 1,5 m C. 2 m D. 3 m
Treść dostępna po opłaceniu abonamentu.Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt ABC. Uzasadnij, że trójkąt ABC jest równoboczny.
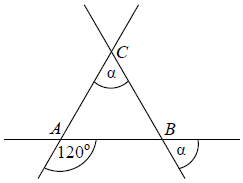Treść dostępna po opłaceniu abonamentu.
Obwód trapezu równoramiennego jest równy 72 cm, ramię ma długość 20 cm, a różnica długości podstaw wynosi 24 cm. Oblicz pole tego trapezu. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.